Analyse der Meeresoberflächentemperaturen von 2023
Bernd Herd
18. Feb 2024
1 Einleitung
Die weltweite mittlere Temperatur hat 2023 enorm zugenommen. In wissenschaftlich interessierten Kreisen wurde dies Seit Juni diskutiert. Der Öffentlichkeit wurde dies im Zusammenhang mit den Überflutungen im Winter 2023 auch im Fernsehen erläutert.
Insbesondere die Darstellung von https://www.climatereanalyzer.org/clim/sst_daily/ wurde diese Jahr in Social Media und auch im ZDF gepostet.
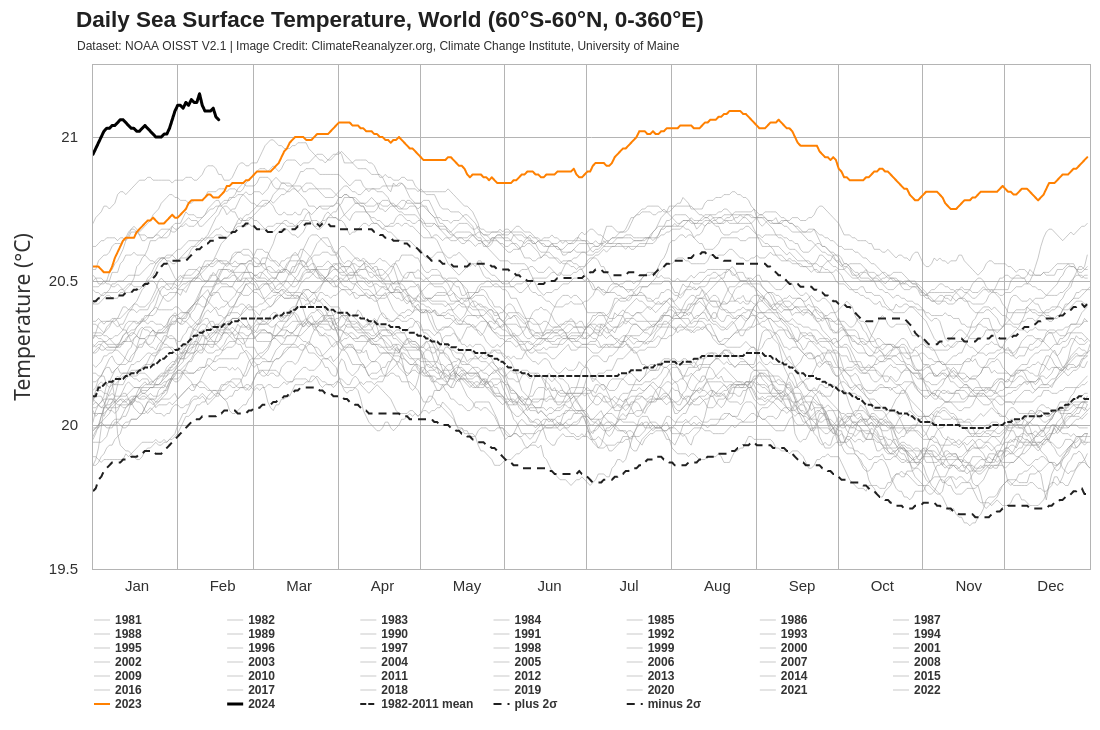
Die Meeresoberflächentemperaturen spielen eine wichige Rolle für das Wetter und spielen wahrscheinlich auch eine Rolle bei den Überflutungen in Deutschland von 2023.
Dazu der ZDF-Meteorologe Terli: https://www.zdf.de/nachrichten/panorama/hochwasser-regen-wetter-niedersachsen-terli-100.html
In diesem Dokument geht es um eine Einordnung der Entwicklung der Meeresoberflächentemperatur im Vergleich zu früheren Jahrzehnten durch eine mathematische Analyse.
2 Werkzeuge
Dieses Dokument basiert auf der Software GNU R https://www.r-project.org/, das unter Debian GNU/Linux ausgeführt wird. Der Quellcode ist erhältlich von https://www.herdsoft.com/ftp/reanalyzer-sst-2024-02-18.zip
3 Analyse der Zeitreihe
Als Ausgangsbasis laden wir die Rohaden von https://www.climatereanalyzer.org/clim/sst_daily/json/oisst2.1_world2_sst_day.json herunter. Sie liegen im JSON-Format vor.
library(jsonlite)
d <- fromJSON("oisst2.1_world2_sst_day.json")Die Daten liegen nun in R als data.frame vor. unter d$name sind den Zeilen die Jahresnamen zugeordnet. Jeder Eintrag umfasst also die Daten eines Jahres. Die letzten drei Einträge sind statistische Auswertungen.
Zunächst mal generieren wir aus den Rohdaten einen Plot, der optisch am die Visualisierung in Climaterealanalyzer angelehnt ist.
plot(d$data[[length(d$name)-3]], type='l', main='Meeresoberflächentemperatur', lwd=3,
ylim=c(19.5, 21.2), ylab='SST °C', xlab='')
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
i=1;
while (i<length(d$name)-5) {
lines(d$data[[i]], type='l', col='lightgray')
i=i+1;
}
lines(d$data[[length(d$name)-4]], type='l', lwd=3, col='orange')
lines(d$data[[length(d$name)-2]], type='l', lty=5)
lines(d$data[[length(d$name)-1]], type='l', lty=2)
lines(d$data[[length(d$name)]], type='l', lty=2)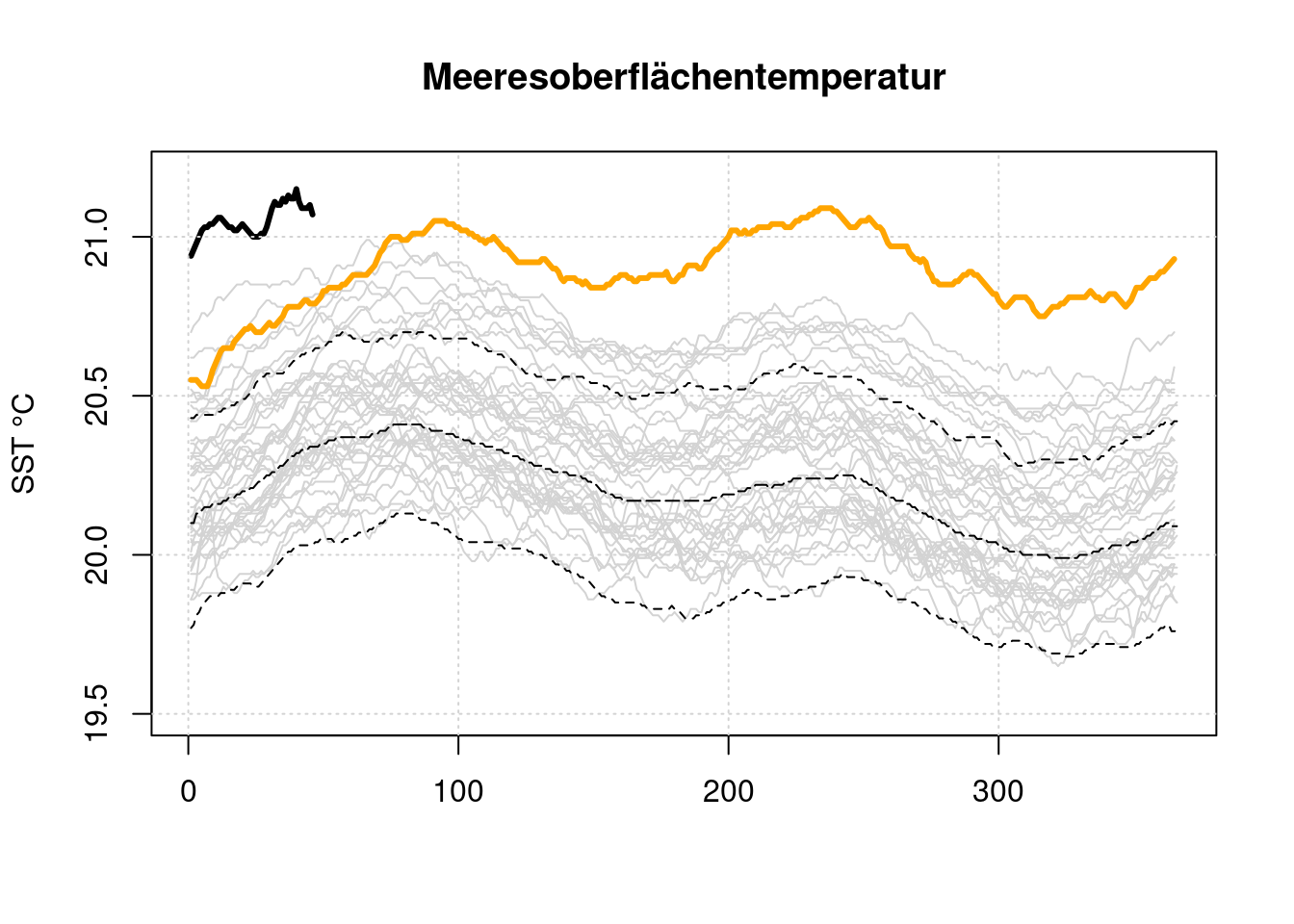
Diese Darstellung betont sehr stark, wie weit die 2023er Kurve oberhalb aller anderen Kurven liegt. Es ist aber nicht erkennbar, ob ein solch schneller Anstrieg der Temperatur auf einem niedrigeren Temperaturniveau in der Vergangenheit auch schon geschehen ist.
Zunächst wandeln wir die nach Jahren organisierten Temperaturen in eine zusammenhängende Zeitreihe ‘timeseries’ um.
Wir bestimmen die Anzahl wirklicher Jahre in Variable years so, dass die Statistikdaten nicht als Jahresdaten falsch interpretiert werden.
years = length(d$name)
while (years > 0 &&
nchar(d$name[years])>4)
{
years=years-1;
}
years;## [1] 44Dabei lassen wir das Jahr 1981 weg, weil dessen Daten im Datensatz unvollständig sind und erst mitten im Jahr beginnen. Wir beginnen also 1982.
startyear = 1;
while (startyear < years &&
d$name[startyear] != "1982")
{
startyear=startyear+1;
}
startyear;## [1] 2timeseries <- 0;
n <- 1;
year <- startyear;
while (year <= years)
{
year_data <- d$data[[year]];
year_data <- year_data[ !is.na(year_data) ];
len <- length(year_data);
timeseries[ n:(n+len-1) ] = year_data;
n = n + len;
year = year + 1;
}
t <- 1982 + 0:(n-2) * (1/365.25)
plot(t, timeseries, type='l', main='Meeresoberflächentemperatur', xlab='', ylab='SST °C')
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))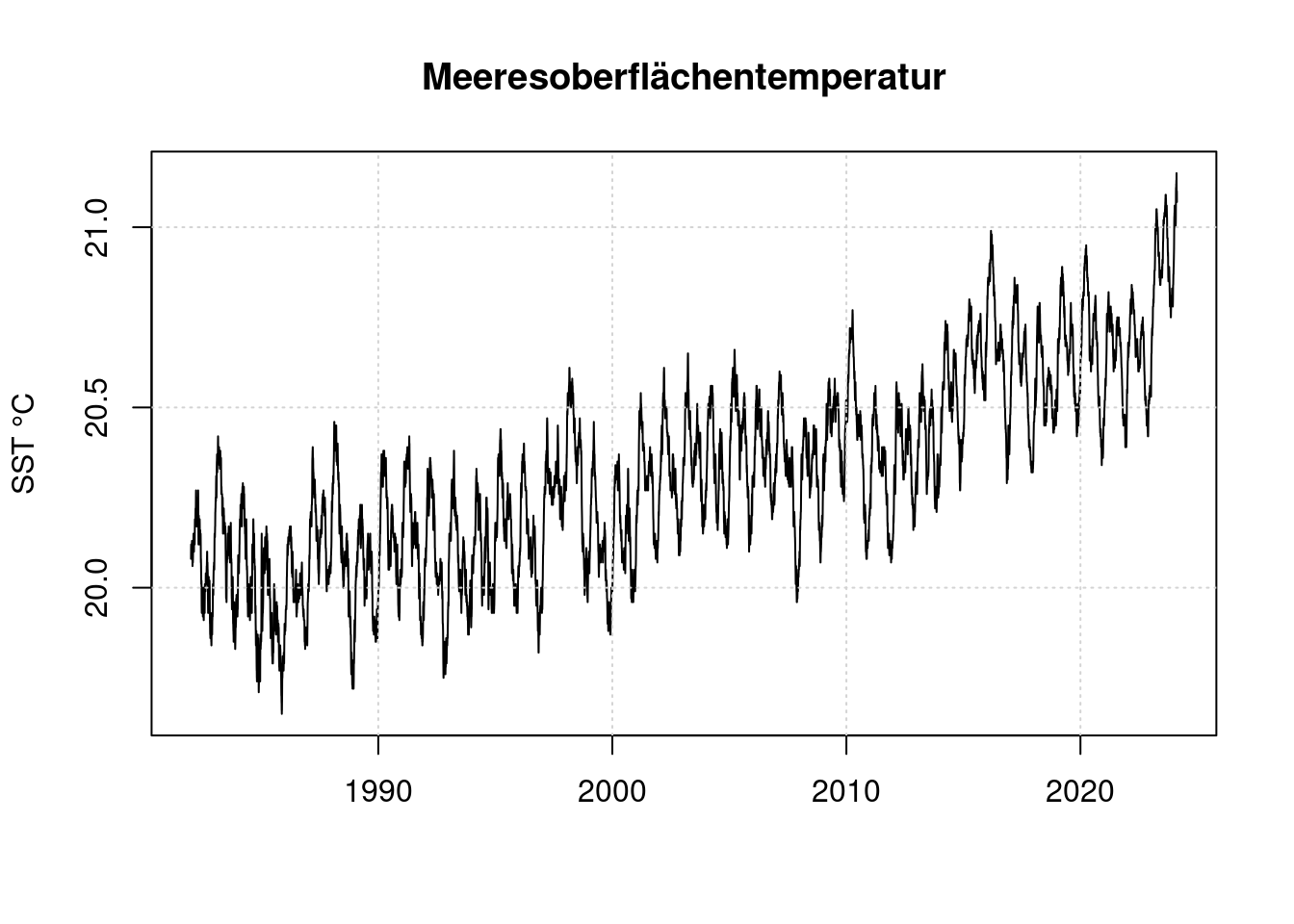
Hier sieht das Extrem von 2023 bei Weitem nicht mehr so beeindruckend aus wie in der Darstellung von clamaterealanyzer.org. Aber der starke Jahresgang versteckt die eigentlichen Unterschiede. Daher bilden wir eine neue Zeitreihe unter Kompensation des Jahresgangs.
4 Berechnung des Jahresgangs
Wir berechnen den Jahresgang als Mittelwert zwischen 1982 und 2022.
season_sum <- rep(0, 365);
year <- 1;
n <- 0;
while (year <= years) {
if (as.numeric(d$name[year]) >= 1982 &&
as.numeric(d$name[year]) <= 2022) {
season_sum = season_sum + d$data[[year]][1:365];
n <- n + 1;
}
year <- year + 1;
}
season_sum[366] <- season_sum[365];
seasonal_avg <- season_sum / n;# Calculate linear time series as anomaly compared to regular seasonal values
anomaly <- 0;
n <- 1;
year = startyear
while (year <= years)
{
year_data <- d$data[[year]];
year_data = year_data-seasonal_avg;
year_data <- year_data[ !is.na(year_data) ];
len <- length(year_data);
anomaly[ n:(n+len-1) ] = year_data;
n = n + len;
year = year + 1;
}
t <- 1982 + 0:(n-2) * (1/365.25)
plot(t, anomaly, type='l',
main='Meeresoberflächentemperatur mit Kompensation des Jahresgangs',
ylab='SST °C', xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))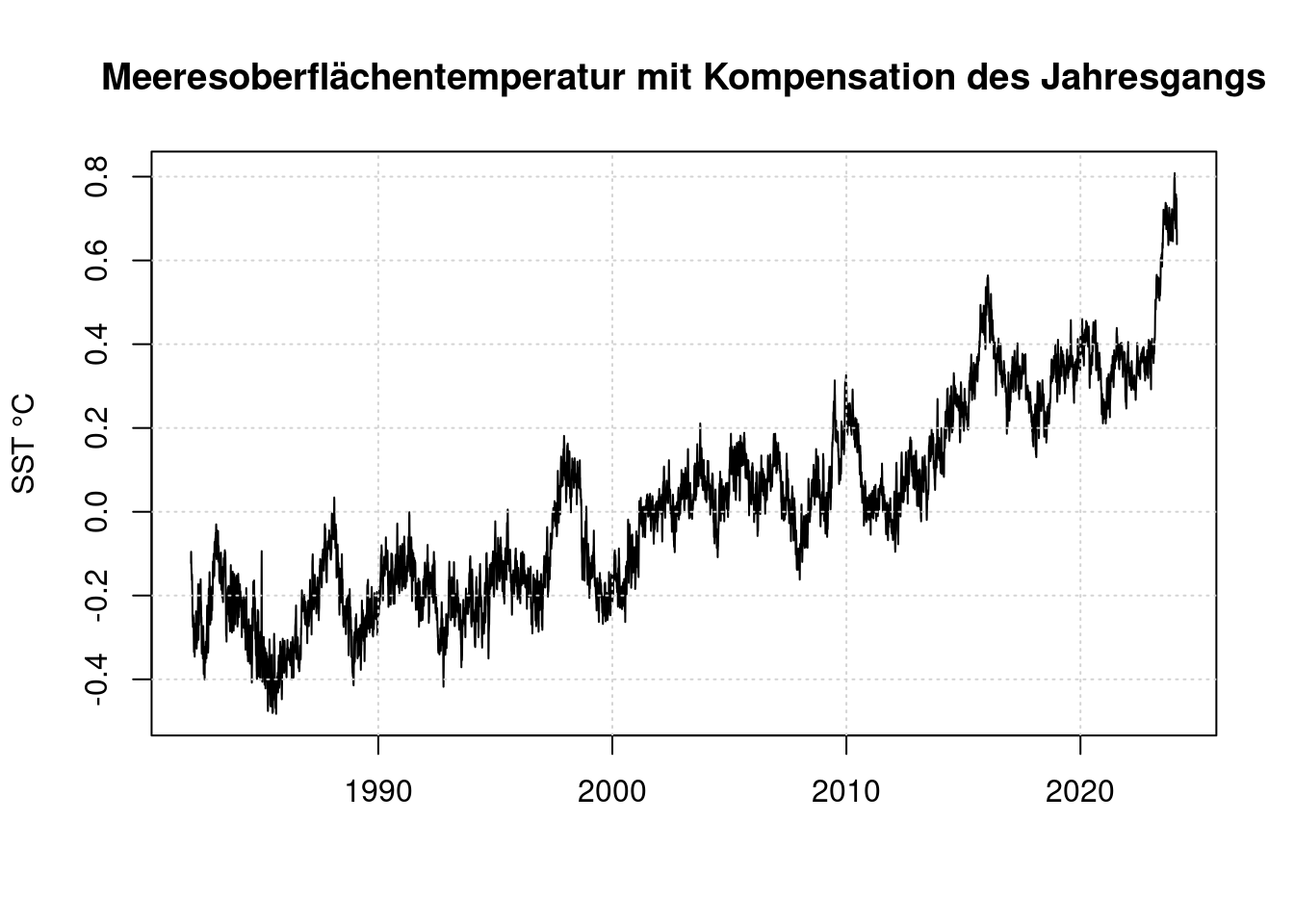
Zunächst ist es nicht überraschend, dass bei stetig steigendem CO2-Anteil in der Atmosphäre die Temperatur stetig steigt. Es fällt auf, dass der Temperaturanstieg 2023 sehr ähnlich aussieht, wie der Temperaturanstieg von 1998:
par(mfcol=c(1, 2));
plot(t, anomaly, xlim=c(1996+0.3,1998+0.3), type='l', ylab='', ylim=c(0.3-0.6,0.9-0.6));
plot(t, anomaly, xlim=c(2022,2024), type='l', ylab='', ylim=c(0.3,0.9))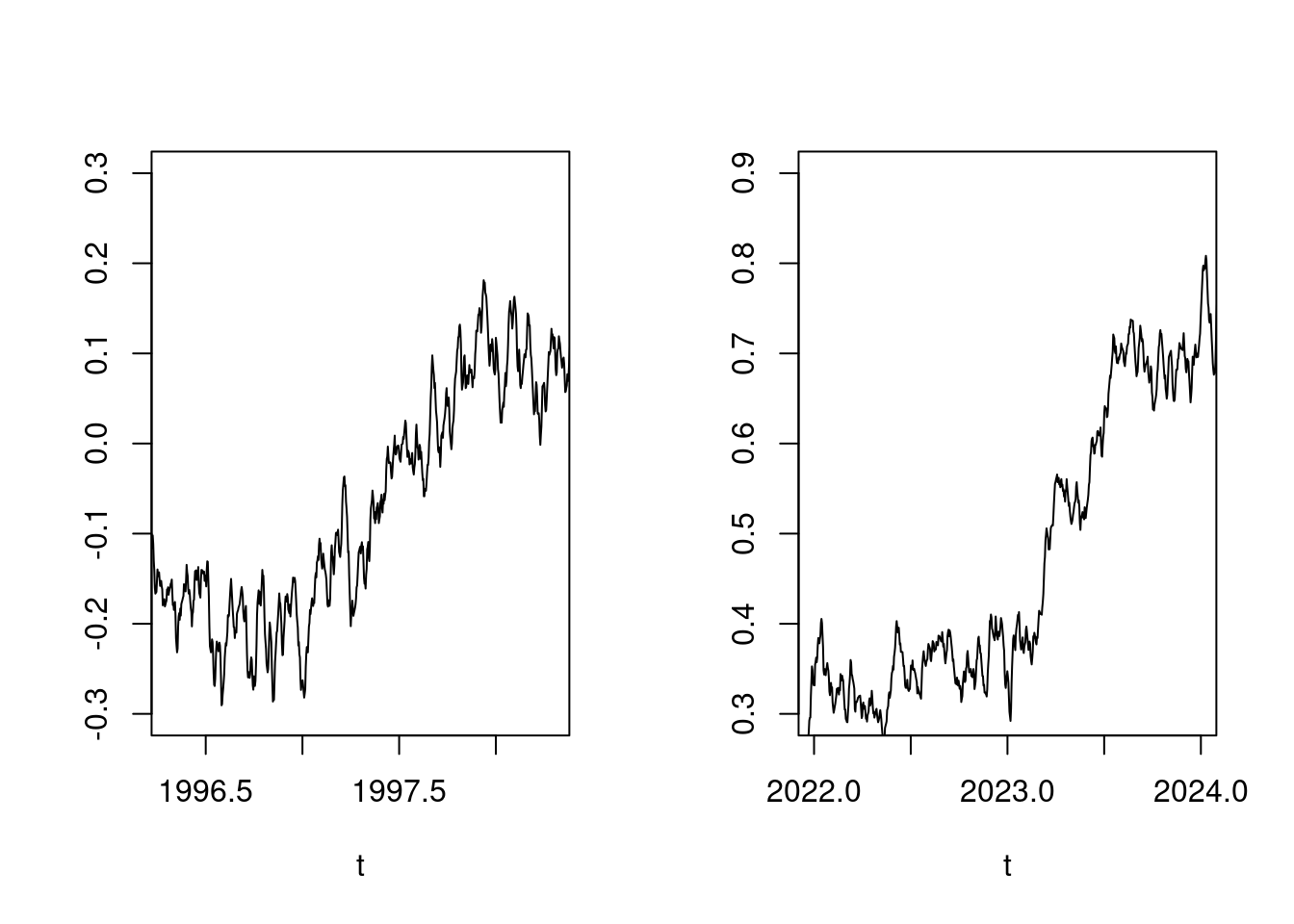
par(mfcol=c(1,1));5 Vergleich 1982-1998 mit 2008-2024
Vergleich des Zetraums bis 1998 mit dem Zeitraum bis 2024 in der Darstellungsweise von climatereanalyzer. Es zeigt sich, dass die beiden Plots sehr ähnlich sind. Nur is die mittlere Meeresoberflächentemperatur seit 1998 um ca. 0,5 °C gestiegen.
drawrange <- function(d, s, e) {
starty <- startyear + s-1982;
endy <- startyear + e-1982;
byday <- 0;
delta_years <- e-s;
daymean <- rep(0, 365);
daysd <- rep(0, 365);
day <- 1
while (day <= 365) {
i=starty;
byday <- rep(0, delta_years);
while (i<endy) {
byday[i-starty+1] <- d$data[[i]][day];
i <- i+1;
}
daymean[day] <- mean(byday);
daysd[day] <- sd(byday);
day <- day+1;
}
plot(d$data[[endy-1]], type='l', main=sprintf('Meeresoberflächentemperatur %d bis %d', s, e), lwd=3, col='orange',
ylim=c(mean(daymean)-0.7, mean(daymean)+0.7), ylab='SST °C', xlab='')
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
i=starty;
while (i<endy-1) {
lines(d$data[[i]], type='l', col='lightgray')
i=i+1;
}
lines(d$data[[endy]][1:80], type='l', lwd=3)
lines(daymean, type='l', lty=2)
lines(daymean+2*daysd, type='l', lty=2)
lines(daymean-2*daysd, type='l', lty=2)
}
drawrange(d, 1982, 1998);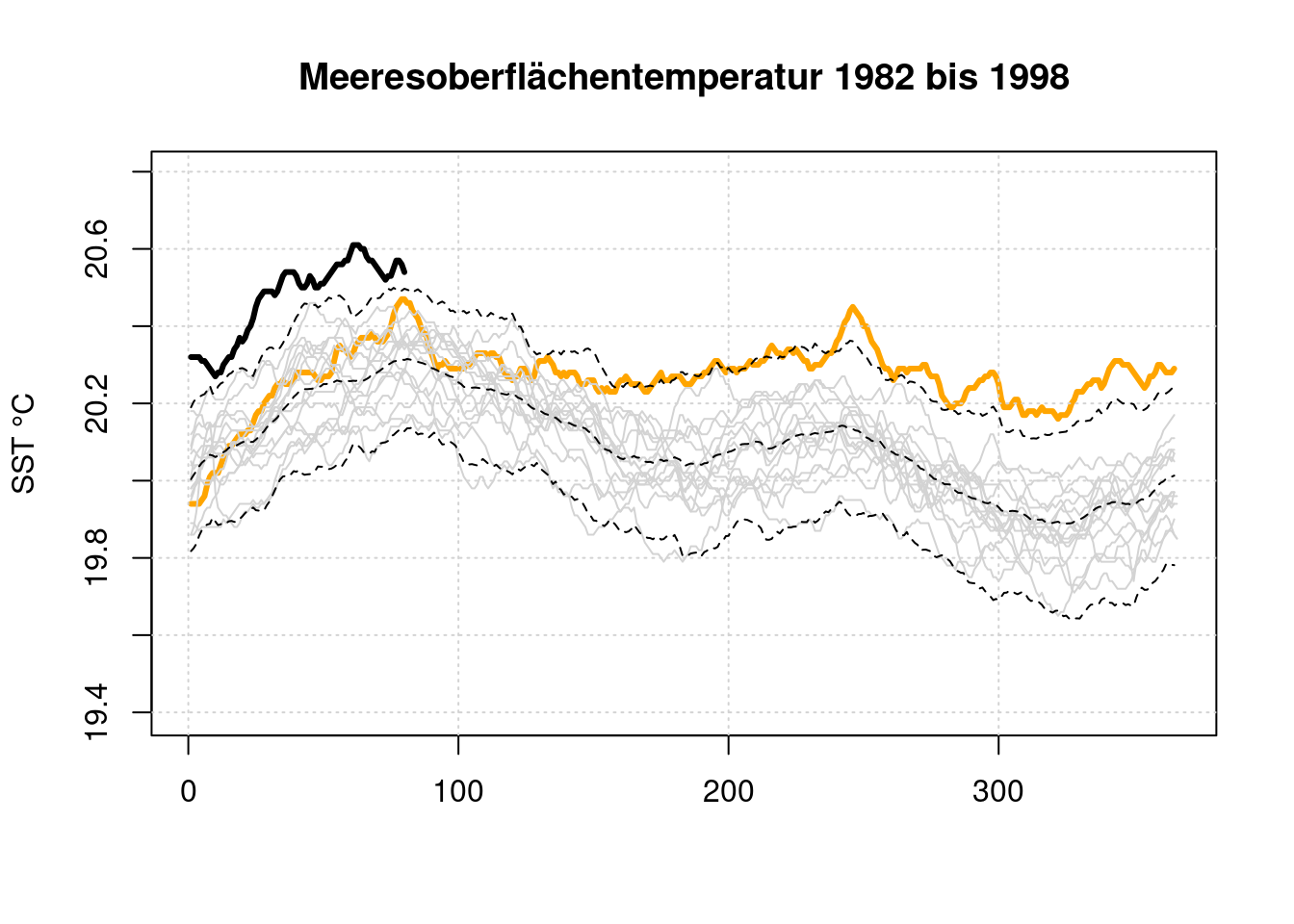
drawrange(d, 2008, 2024);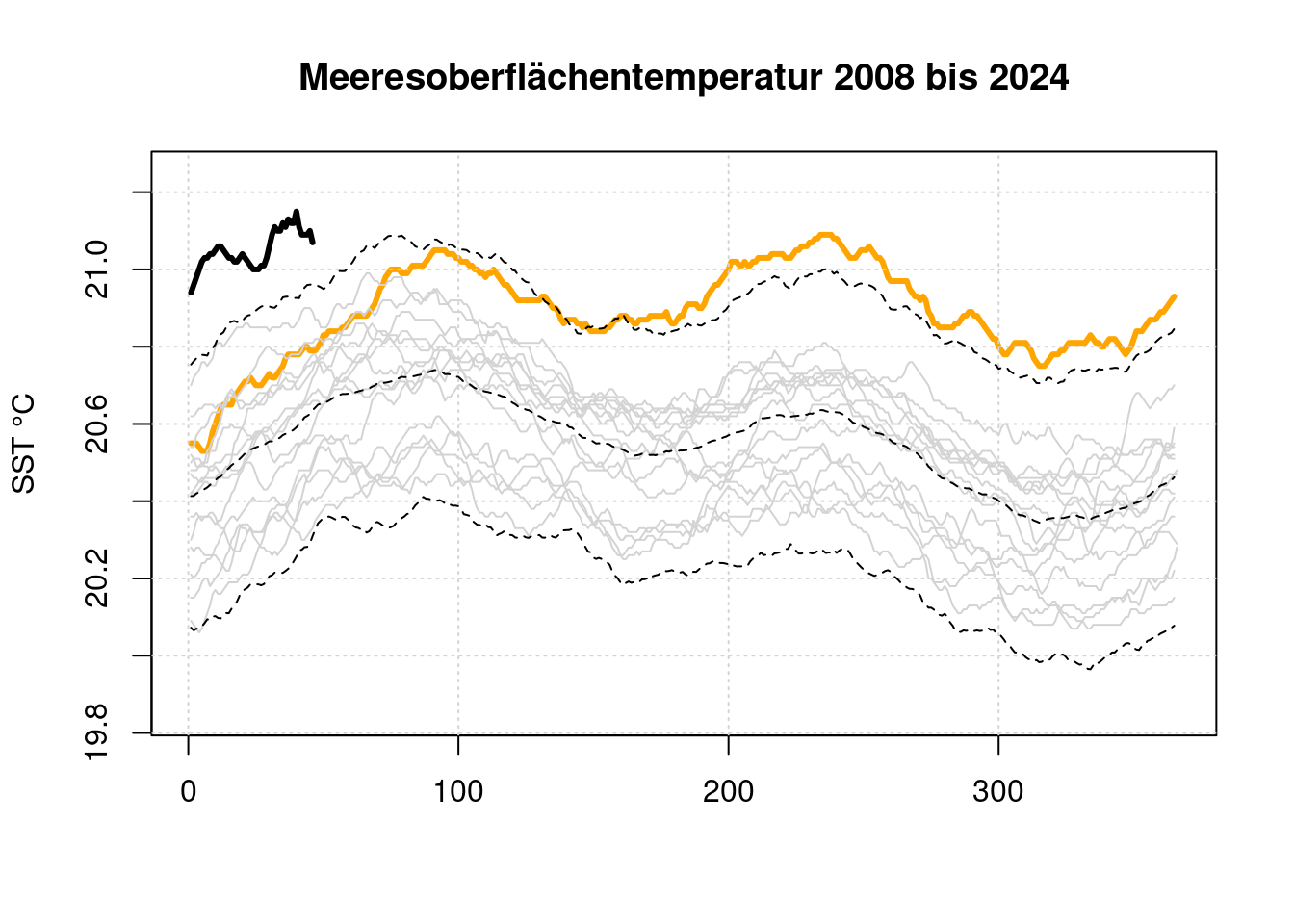
Die Ursache hierfür ist, dass sowohl 1998, als auch 2023 Jahre mit einem Starken ENSO (El Niño Southern Oscillation) waren.
6 ENSO
Seit 1979 gibt es Zeitreihenaufzeichnungen zum Status der El Niño Southern Oscilation. Wir laden diese herunter von: https://psl.noaa.gov/enso/mei/data/meiv2.data
Danach bilden wir daraus wieder eine Zeitreihe mit Tagen ab 1982.
raw_enso <- read.table(pipe("tail --lines=+2 meiv2.data|egrep '^19|^20'"),
sep="", header=F);
raw_enso$year <- raw_enso$V1; raw_enso$V1 <- NULL;
n_enso <- length(raw_enso$V2)
if (raw_enso$V3[n_enso] == -999) { raw_enso$V3[n_enso] <- raw_enso$V2[n_enso] }
if (raw_enso$V4[n_enso] == -999) { raw_enso$V4[n_enso] <- raw_enso$V3[n_enso] }
if (raw_enso$V5[n_enso] == -999) { raw_enso$V5[n_enso] <- raw_enso$V4[n_enso] }
if (raw_enso$V6[n_enso] == -999) { raw_enso$V6[n_enso] <- raw_enso$V5[n_enso] }
if (raw_enso$V7[n_enso] == -999) { raw_enso$V7[n_enso] <- raw_enso$V6[n_enso] }
if (raw_enso$V8[n_enso] == -999) { raw_enso$V8[n_enso] <- raw_enso$V7[n_enso] }
if (raw_enso$V9[n_enso] == -999) { raw_enso$V9[n_enso] <- raw_enso$V8[n_enso] }
if (raw_enso$V10[n_enso] == -999) { raw_enso$V10[n_enso] <- raw_enso$V9[n_enso] }
if (raw_enso$V11[n_enso] == -999) { raw_enso$V11[n_enso] <- raw_enso$V10[n_enso] }
if (raw_enso$V12[n_enso] == -999) { raw_enso$V12[n_enso] <- raw_enso$V11[n_enso] }
if (raw_enso$V13[n_enso] == -999) { raw_enso$V13[n_enso] <- raw_enso$V12[n_enso] }
enso <- 1;
i = 4; # raw_enso$year[4] == 1982
n = 1
while (i <= length(raw_enso$year))
{
enso[n:(n+30)] <- rep(raw_enso$V2[i], 31); n <- n+31; # Januar
if ( (raw_enso$year[i] %% 4) == 0 ) {
enso[n:(n+28)] <- rep(raw_enso$V3[i], 29); n <- n+29; # Februar
} else {
enso[n:(n+27)] <- rep(raw_enso$V3[i], 28); n <- n+28; # Februar
};
enso[n:(n+30)] <- rep(raw_enso$V4[i], 31); n <- n+31; # März
enso[n:(n+29)] <- rep(raw_enso$V5[i], 30); n <- n+30; # April
enso[n:(n+30)] <- rep(raw_enso$V6[i], 31); n <- n+31; # Mai
enso[n:(n+29)] <- rep(raw_enso$V7[i], 30); n <- n+30; # Juni
enso[n:(n+30)] <- rep(raw_enso$V8[i], 31); n <- n+31; # Juli
enso[n:(n+30)] <- rep(raw_enso$V9[i], 31); n <- n+31; # August
enso[n:(n+29)] <- rep(raw_enso$V10[i], 30); n <- n+30; # September
enso[n:(n+30)] <- rep(raw_enso$V11[i], 31); n <- n+31; # Oktober
enso[n:(n+29)] <- rep(raw_enso$V12[i], 30); n <- n+30; # November
enso[n:(n+30)] <- rep(raw_enso$V13[i], 31); n <- n+31; # Dezember
i = i+1;
}
# Fill up ENSO Vector if it is shorter
if (length(enso) < length(anomaly)) {
enso[(length(enso)+1):length(anomaly)] <- enso[length(enso)]
}
enso <- enso[ 1:(length(anomaly)) ];
plot(t, enso, main='El Niño Southern Oscillation Index', type='l', xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))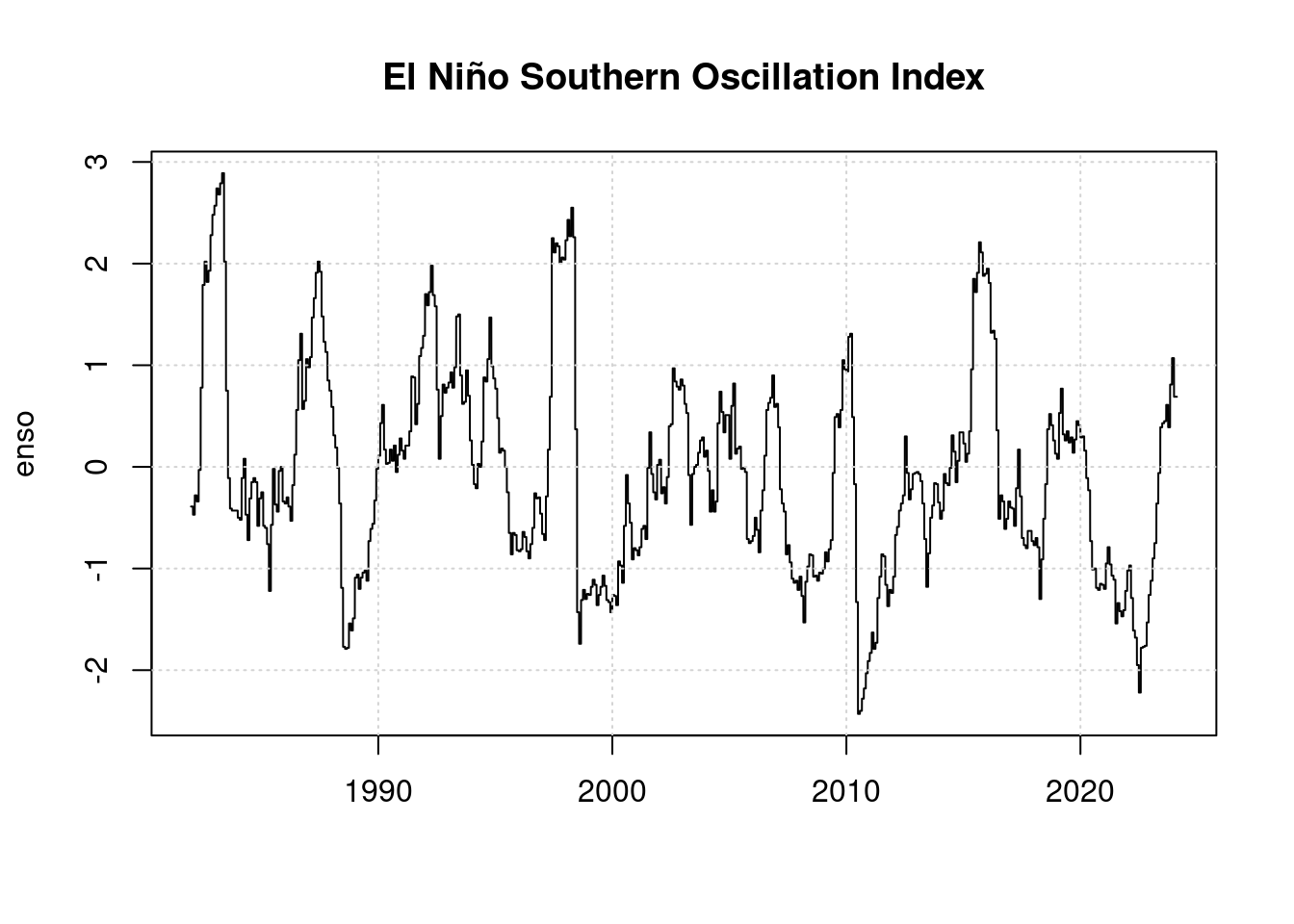
Bemerkenswert ist, dass sich 2023 ein El Niño zu entwickeln beginnt, der Index ist bislang aber nur leicht positiv, weit niedriger als 2016 oder gar 1998. Daher wurde 2023 von Wissenschaftlern nicht als El Niño Jahr eingestuft.
7 CO2
Die Veränderung des CO2-Gehalts in der Atmosphäre laden wir von ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_weekly_mlo.csv Die Datei enthält wöchentliche Angaben der auf Mauna Loa gemessenen CO2-Konzentration. Es gibt Lücken in der Aufzeichnung, die wir bei der Umwandlung in eine Zeitreihe auffüllen müssen.
co2_weekly <- read.table(pipe("grep -v '^#' co2_weekly_mlo.csv"), sep=",", header=T);
co2 <- rep(0,8);
i <- 1;
n <- 1;
while (i <= length(co2_weekly$decimal))
{
if (co2_weekly$decimal[i] > 1982)
{
x <- (co2_weekly$decimal[i] - 1982) * 365.25;
if (co2_weekly$average[i]>0) {
co2[x:(x+7)] = rep(co2_weekly$average[i], 8);
} else {
co2[x:(x+7)] = rep(co2[length(co2)], 8);
}
}
i = i+1;
}
co2[1] <- co2[2];
if (length(co2) < length(t)) {
co2[(length(co2)+1):length(t)] <- co2[length(co2)];
}
co2 <- co2[1:(length(anomaly))];
plot(t, co2, main='CO~2~ Konzentratin in Parts per Million', type='l');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))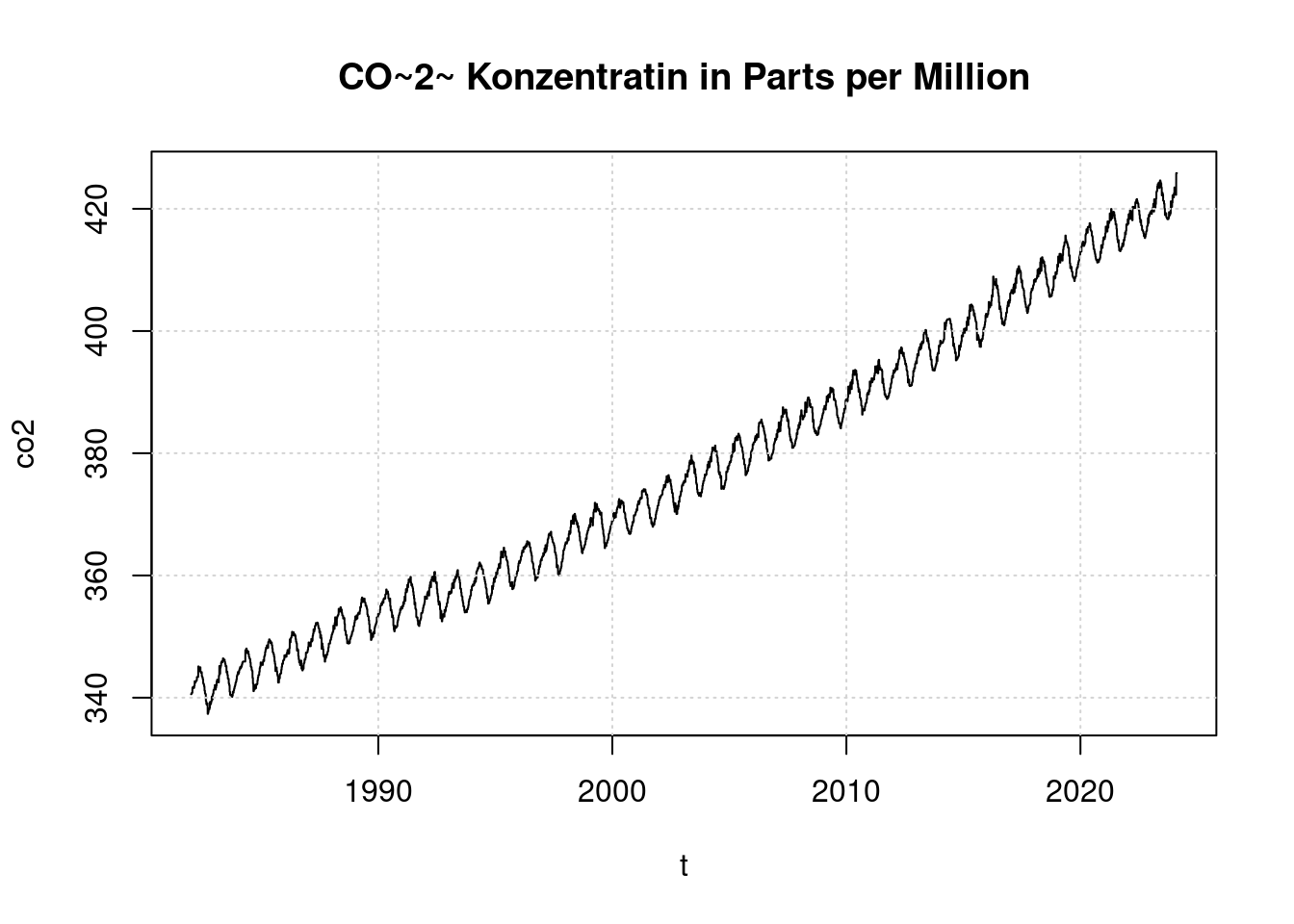
8 Sonnenaktivität
Ein weiterer bekannter Einflußfaktor auf die Erdtemperatur ist die Sonnenaktivität, die typischerweise in ihrer Stärke einen 11-Jährigen Zyklus aufweist. Die Sonnenaktivität kann anhand der Anzahl von Sonnenflecken grob abgeschätzt werdem
Wir laden diese Daten von http://www.sidc.be/silso/DATA/SN_y_tot_V2.0.txt und wandeln sie in eine tagesweise Zeitreihe um.
library(interp);
sun_yearly <- read.table(pipe("sed 's/\\*$//' SN_y_tot_V2.0.txt"), sep="", header=F);
sun_yearly$year <- sun_yearly$V1; sun_yearly$V1<-NULL;
sun_yearly$sunspots <- sun_yearly$V2; sun_yearly$V2<-NULL;
sunspots <- aspline((1982-sun_yearly$year[1]+1):(length(sun_yearly$year)), sun_yearly$sunspots[283:(length(sun_yearly$year))], n=length(anomaly))$y;
plot(t, sunspots, main='Anzahl Sonnenflecken', type='l', lwd=3);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))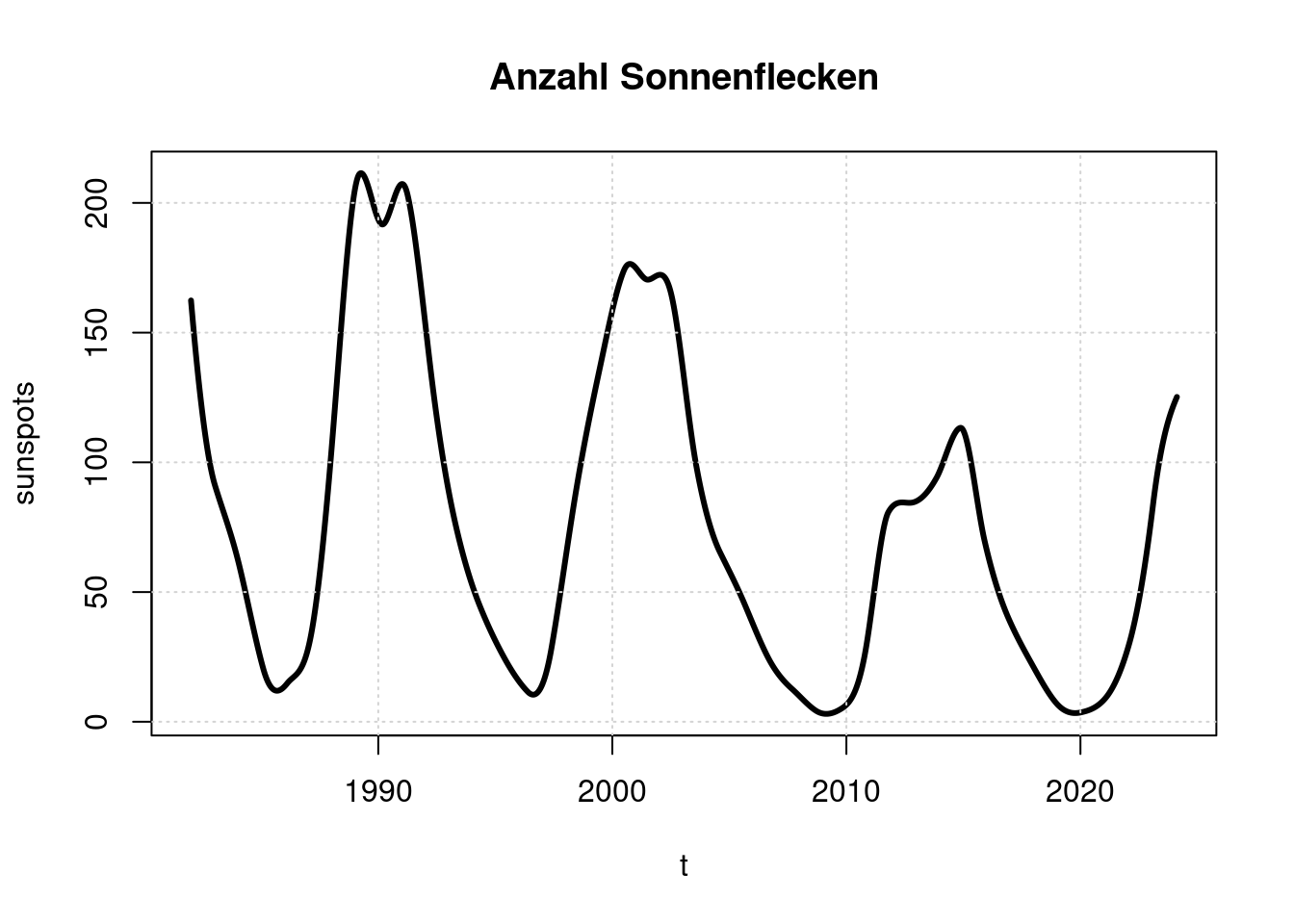
9 Gegenüberstellung
Zur Gegenüberstellung der Einflussgrößen wandeln wir die Daten in einen data.frame um und benutzen xyplot aus dem Lattice Paket. Die gewählten Faktoren sind zunächst absolut willkürlich.
library(lattice);
df <- data.frame(t, anomaly, enso, co2, sunspots)
xyplot(anomaly+enso*0.1+(log(co2/280)-0.3)*4+(sunspots*0.001)~t, data = df, ylab='',
main = 'Gegenüberstellung der Einflussgrößen', type='l', auto.key=TRUE);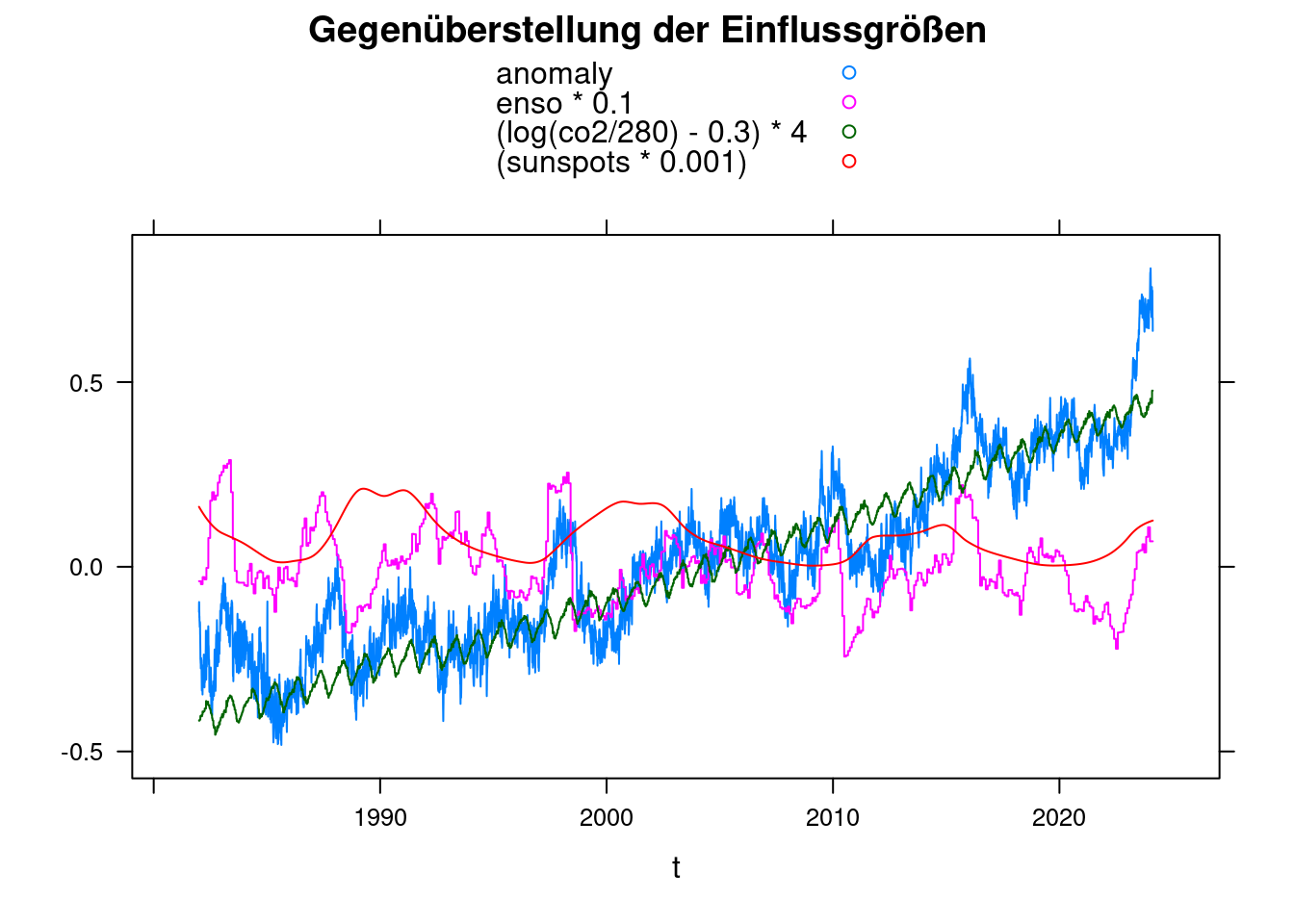
10 Parameter eines Modells
Um zu erkennen, ob es 2023 einen unbekannten Einflußfaktor für die Meeresmitteltemperatur gegeben hat, bestimmen wir mit einem mathematischen Modell, wie gut sich die gemessenen Temperaturen aus den bereits bekannten Einflußgrößen ableiten lassen.
tfit <- nls(anomaly ~ A + B*log(co2/280) + C*enso +D*sunspots, data = df,
start = list( A=mean(df$anomaly), B=0.01, C=0, D=0) );
tfit;## Nonlinear regression model
## model: anomaly ~ A + B * log(co2/280) + C * enso + D * sunspots
## data: df
## A B C D
## -1.1320998 3.8352571 0.0598153 0.0001994
## residual sum-of-squares: 104.9
##
## Number of iterations to convergence: 1
## Achieved convergence tolerance: 9.938e-08plot(df$t, df$anomaly, type='l', col='blue', lwd=1, xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
lines(predict(tfit) ~ df$t, type='l', col="darkgreen", lwd=3);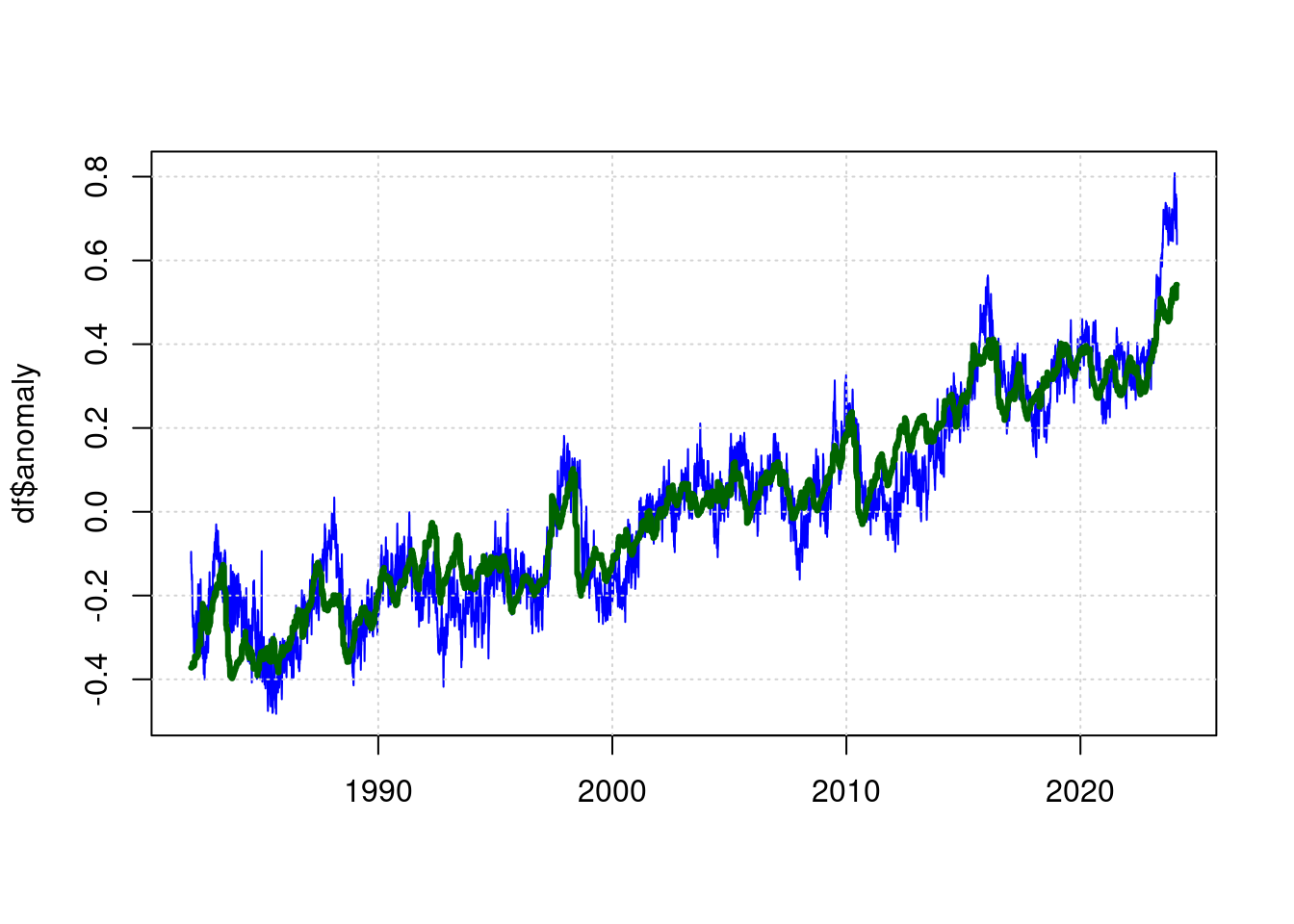
Die grüne Linie ist nun der Schätzwert für die erwartete Temperatur anhand der Parameter (CO2, ENSO, Sunspots) und die Blaue Linie ist die gemessene Temperatur.
11 Filterung
Es zeigt sich, dass eine Tiefpass-Filterung der Werte von ENSO und CO2 das Modell noch ein wenig verbessert. Der Wert “residual sum-of-squares” im NLS-Ergebnis wird dadurch kleiner.
Zur Filterung verwenden wir einen einfachen IIR-Filter (Infinite-Impulse-Response):
lowpass <- function(inp, lambda) {
value <- mean(inp[1:20]);
result <- 0;
i <- 1;
while (i<=length(inp))
{
value = value*(1-lambda) + inp[i]*lambda;
result[i] = value;
i = i+1;
}
result;
}Jetzt ergänzen wir gefilterte Werte für enso und co2 im Dataframe df:
df$fco2 <- lowpass(df$co2, 0.012);
df$fenso <- lowpass(df$enso, 0.012);Und wir aktualisieren unser Modell:
ffit <- nls(anomaly ~ A + B*fco2 + C*fenso +D*sunspots, data = df, start = list( A=mean(df$anomaly), B=0.01, C=0, D=0) );
ffit;## Nonlinear regression model
## model: anomaly ~ A + B * fco2 + C * fenso + D * sunspots
## data: df
## A B C D
## -3.9630554 0.0105134 0.0776045 0.0002919
## residual sum-of-squares: 83.76
##
## Number of iterations to convergence: 2
## Achieved convergence tolerance: 1.697e-09plot(df$t, df$anomaly, type='l', col='blue', lwd=1);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
lines(predict(ffit) ~ df$t, type='l', col="darkgreen", lwd=3);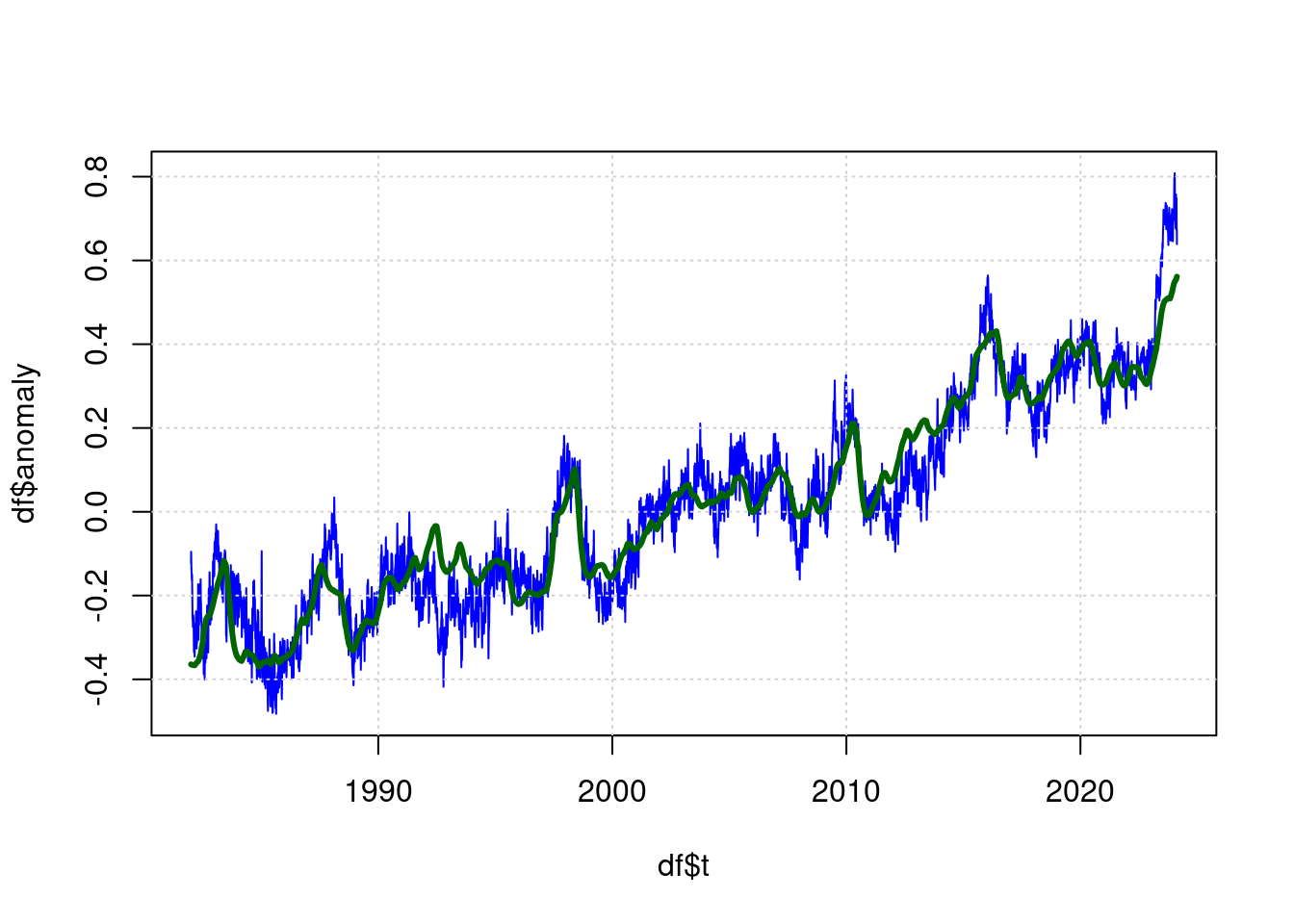
12 Das Residuum
Der Teil des Messergebnisses, der nach dem Modell nicht aus den Eingangswerten abgeleitet werden kann, sieht damit so aus:
residuum <- anomaly - predict(ffit);
plot(df$t, residuum, type='l', col='blue', lwd=1);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))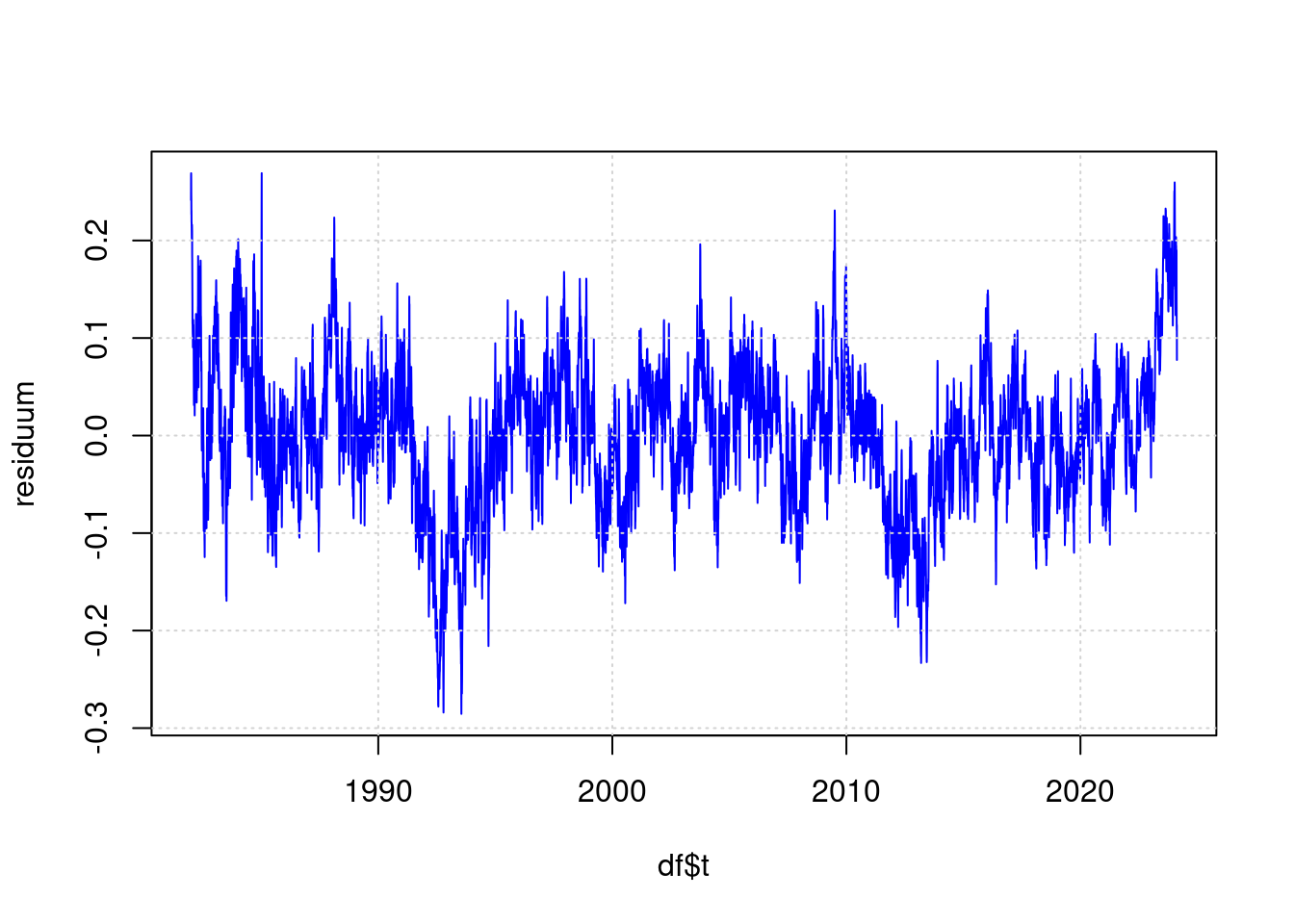
Hier sieht das hohe Messergebnis von 2023 bei weitem nicht mehr so beeindruckend aus wie in der ursprünglichen Visualisierung.
13 Gegenüberstellung
fval<-coef(ffit);
xyplot(anomaly+(fco2*fval[2]+fval[1])+fenso*fval[3]+sunspots*fval[4]~t, data = df,
main = 'Gegenüberstellung Einflußgrößen', type='l', auto.key=TRUE);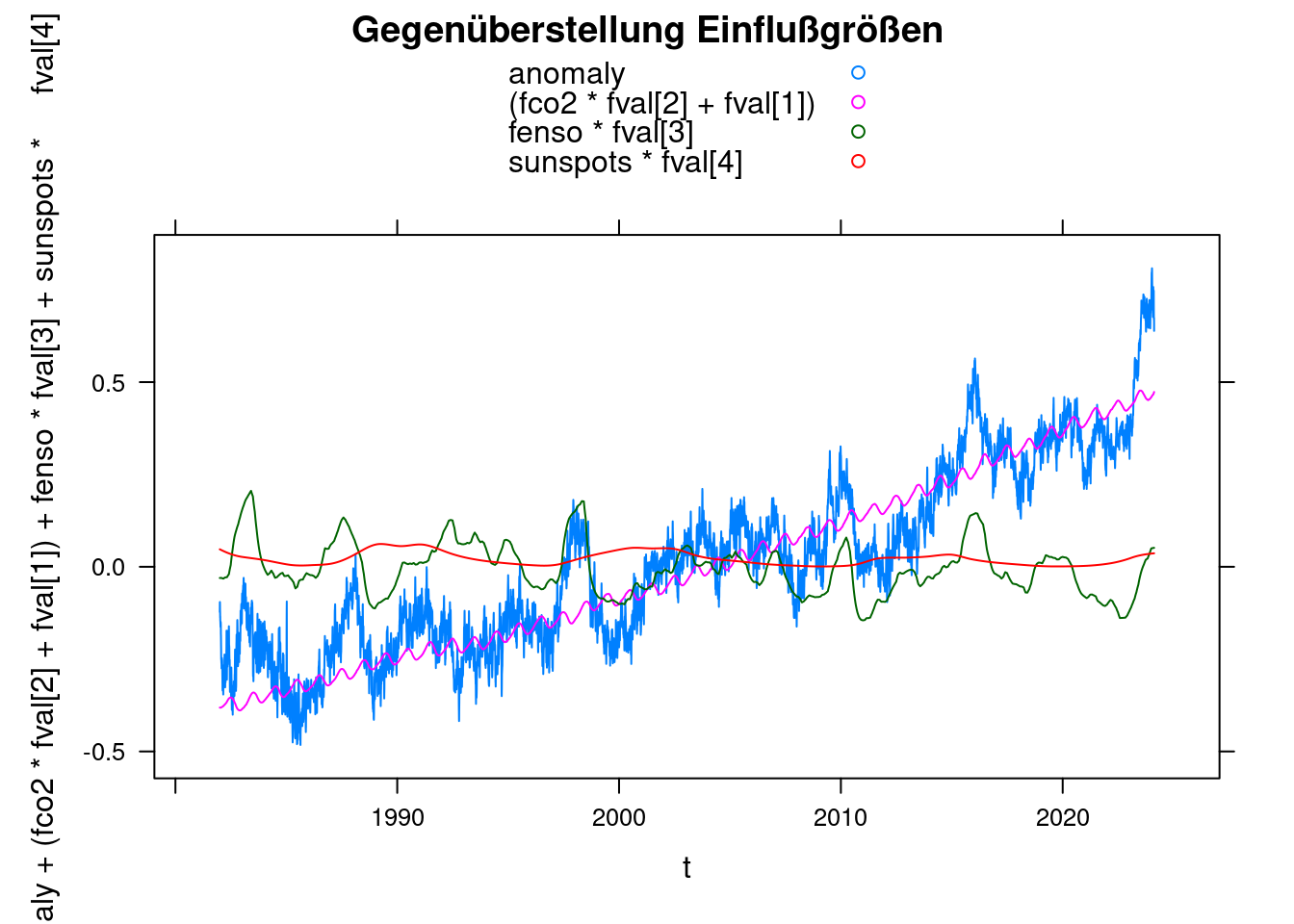
14 Tagesrauschen ausfiltern
Da das Rauschen den Plot schwer erkennbar macht, wenden wir die Tiefpassfilterung noch auf die messwerte “anomalie” an, um einen glatteren Plot zu erhalten:
df$fanomaly <- lowpass(df$anomaly, 0.025);
xyplot(fanomaly+(fco2*fval[2]+fval[1])+fenso*fval[3]+sunspots*fval[4]~t, data = df,
main = 'Gegenüberstellung Einflußgrößen', type='l', auto.key=TRUE);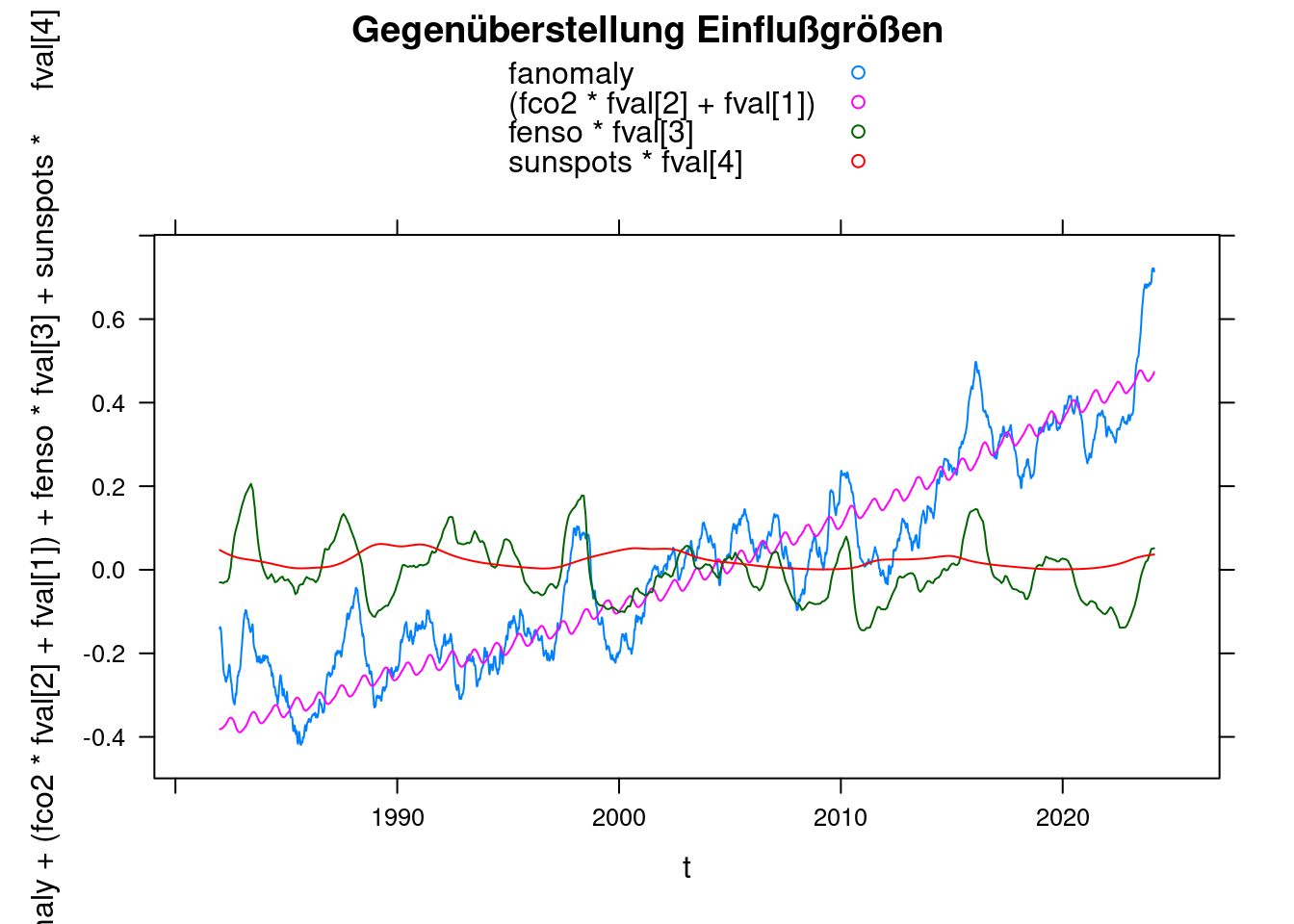
Dasselbe für das Residuum
fresiduum <- lowpass(residuum, 0.025);
plot(df$t, fresiduum, type='l', col='blue', lwd=1);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))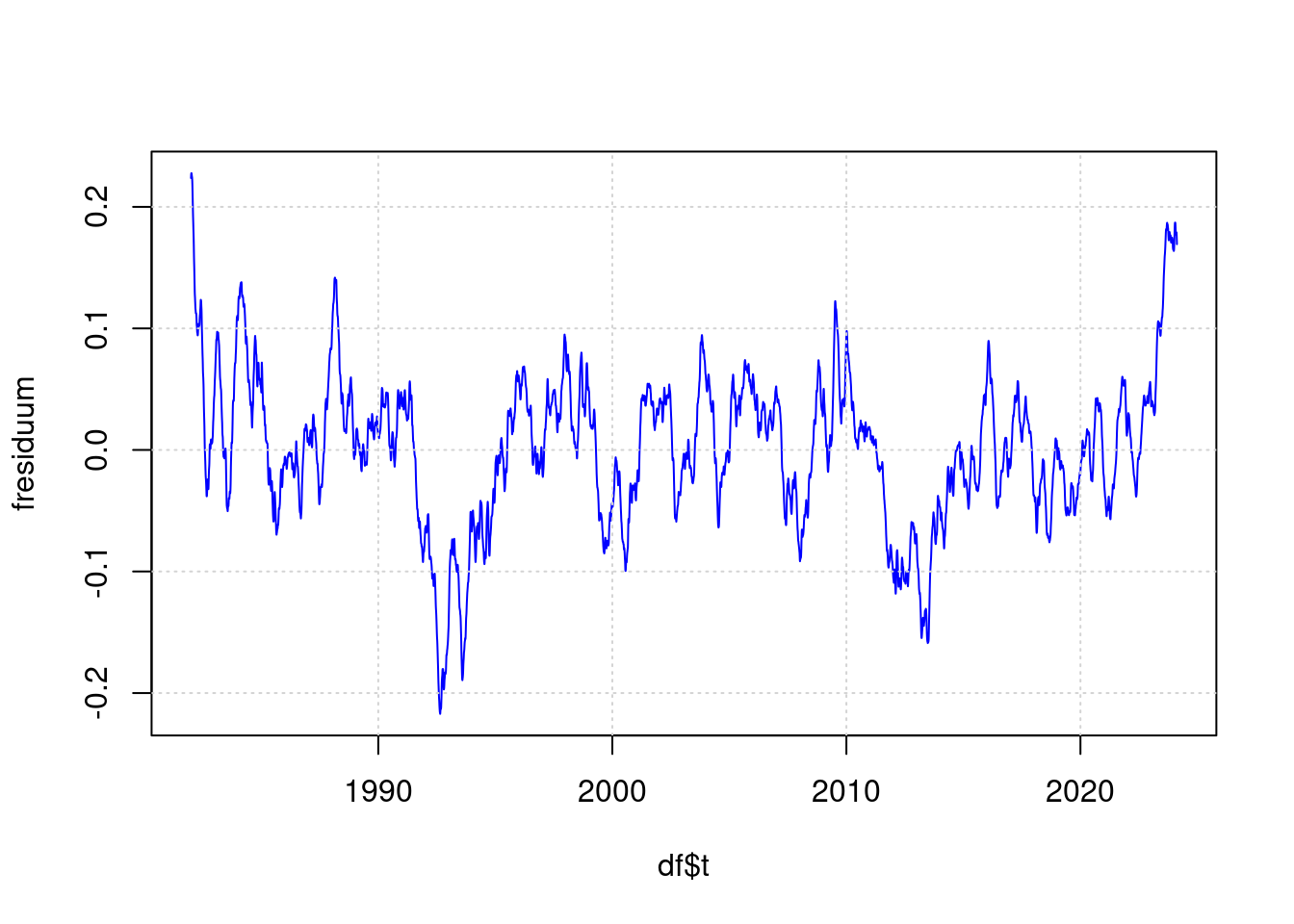
15 Statistik
Die Standardabweichung des Residuums beträgt:
standard_deviation = sd(residuum);
standard_deviation;## [1] 0.07378745Der höchste Wert des Residuums beträgt damit in Standardabweichungen (Sigma):
max(residuum / standard_deviation);## [1] 3.64634min(residuum / standard_deviation);## [1] -3.867823Die Wahrscheinlichkeit, dass ein Wert in einer Meßreihe diesen Wert erreicht, beträgt:
pnorm(-max(residuum)/standard_deviation);## [1] 0.000133001Das sieht erst mal sehr wenig aus, aber unsere Zeitreihe enthält ja auch Messungen für jeden Tag aus mehreren Jahrzehnten. Dementsprechend ist zu erwarten, dass dieser maximalwert im Mittel an
pnorm(-max(residuum)/standard_deviation) * length(residuum);## [1] 2.046353Tagen erreicht wird.
Ein Wert von +0.21 Grad wurde erreicht an:
sum(residuum > 0.21)## [1] 57Tagen.
Zu erwarten sind laut Statistik:
pnorm(-0.21/standard_deviation) * length(residuum);## [1] 34.0572816 Fazit
Zunächst mal ist es wenig überraschend, dass die Erde sich wie seit Jahrzehnten vorhergesagt erwärmt. Die zugrundelegenden Mechanismen sind wissenschaftlich gut verstanden und lassen auch Aussagen über die Zukunft zu.
Die 2023 Meßergebnisse sind jedenfalls kein überzeugender Grund zu der von Hansen postulierten Annahme, dass der IPCC seit Jahrzehnten die Klimasensitivität gravierend unterschätzen würde.
Die Werte von 2023 und Anfang 2024 liegen um ca. 0,2°C höher als es nach den bekannten Einflußfaktoren zu erwaten wäre. Aber das ist noch nicht so ungewöhnlich, dass das zwangsläufig an einem neuen Einflußfaktor liegen müsste.
So lange die Menschheit weiter so viel CO2 emittiert, werden sich auch die Meere weiter erwärmen. Mit entsprechenden Folgen.
