Kreditentwicklung Bürstadt 1997 bis 2024
Bernd Herd
16. Nov 2024
1 Einleitung
Die Verschuldung hat der Kommune Bürstadt hat sich seit 2019 stark erhöht.
Alle Informationen in diesem Text sind aus öffentlichen Quellen und genauestens dokumentiert.
2 Entwicklung der Verschuldung
Dokumente zur Schuldenentwicklung der Stadt Bürstadt sind öffentlich und eindeutig.
Entwurf Haushaltsplan 2024 vom 8.11.23 Seite 35.
https://www.buerstadt.de/de/rathaus-politik/rathausservice/haushaltsplan#c363
https://www.buerstadt.de/fileadmin/Dateien/Dateien/Rathaus_und_Politik/Haushaltsplan/Haushaltsplan_2020.pdf Bilanz Verbindlichkeiten aus Kreditaufnahmen zum 31.12.2018: 17.444.571,12 31.12.2017: 16.567.977,11
https://www.buerstadt.de/fileadmin/Dateien/Dateien/Rathaus_und_Politik/Haushaltsplan/20190711_Haushaltsplan_Haushalt_2019.pdf Bilanz Verbindlichkeiten aus Kreditaufnahmen 2017 16.567.977,11 2016 18.059.767,27
https://www.buerstadt.de/fileadmin/Dateien/Dateien/Rathaus_und_Politik/Haushaltsplan/20190711_Haushaltsplan_Haushalt_2018.pdf Bilanz Verbindlichkeiten aus Kreditaufnahmen 31.12.2016 18.059.767,27 31.12.2015 19.666.125,70
https://www.buerstadt.de/fileadmin/Dateien/Dateien/Rathaus_und_Politik/Haushaltsplan/20190711_Haushaltsplan_Haushalt_2017.pdf Bilanz Verbindlichkeiten aus Kreditaufnahmen 31.12.2014 19.532.359,03 € 31.12.2013 18.601.538,40 €
Der Plot zeichnet den Schuldenstand jeweils am Anfang eines Jahres. D.h. z.B. der Kringel bei 2024 gibt den Schuldenstand zum 31.12.2023 an. Der Wert für Anfang 2025 ist die Planung nach dem Haushalt 2024.
d <- read.table('kreditentwicklung-2024.csv', header=TRUE, sep="\t")
d$endbestand <- NULL
d$Neuaufnahme <- NULL
d$Tilgung <- NULL
d$Neuverschuldung <- NULL
d$Pro.Kopf. <- NULL
d$Stand <- NULL
d$Quelle <- NULL
d <- subset(d, jahr > 2013 & jahr<=2025)
knitr::kable(d);| jahr | anfangsbestand | |
|---|---|---|
| 2 | 2014 | 18601538 |
| 3 | 2015 | 19532359 |
| 4 | 2016 | 19666126 |
| 5 | 2017 | 18059767 |
| 6 | 2018 | 16567977 |
| 7 | 2019 | 17400412 |
| 8 | 2020 | 18174247 |
| 9 | 2021 | 23125640 |
| 10 | 2022 | 26913000 |
| 11 | 2023 | 31508080 |
| 12 | 2024 | 33360080 |
| 13 | 2025 | 36364810 |
plot(d$jahr, d$anfangsbestand/(1000*1000), type='b', ylim=c(0, max(d$anfangsbestand)/(1000*1000)),
main='Verbindlichkeiten aus Kreditaufnahme Bürstadt',
xlab='Jahr', ylab='Millionen EUR')
grid();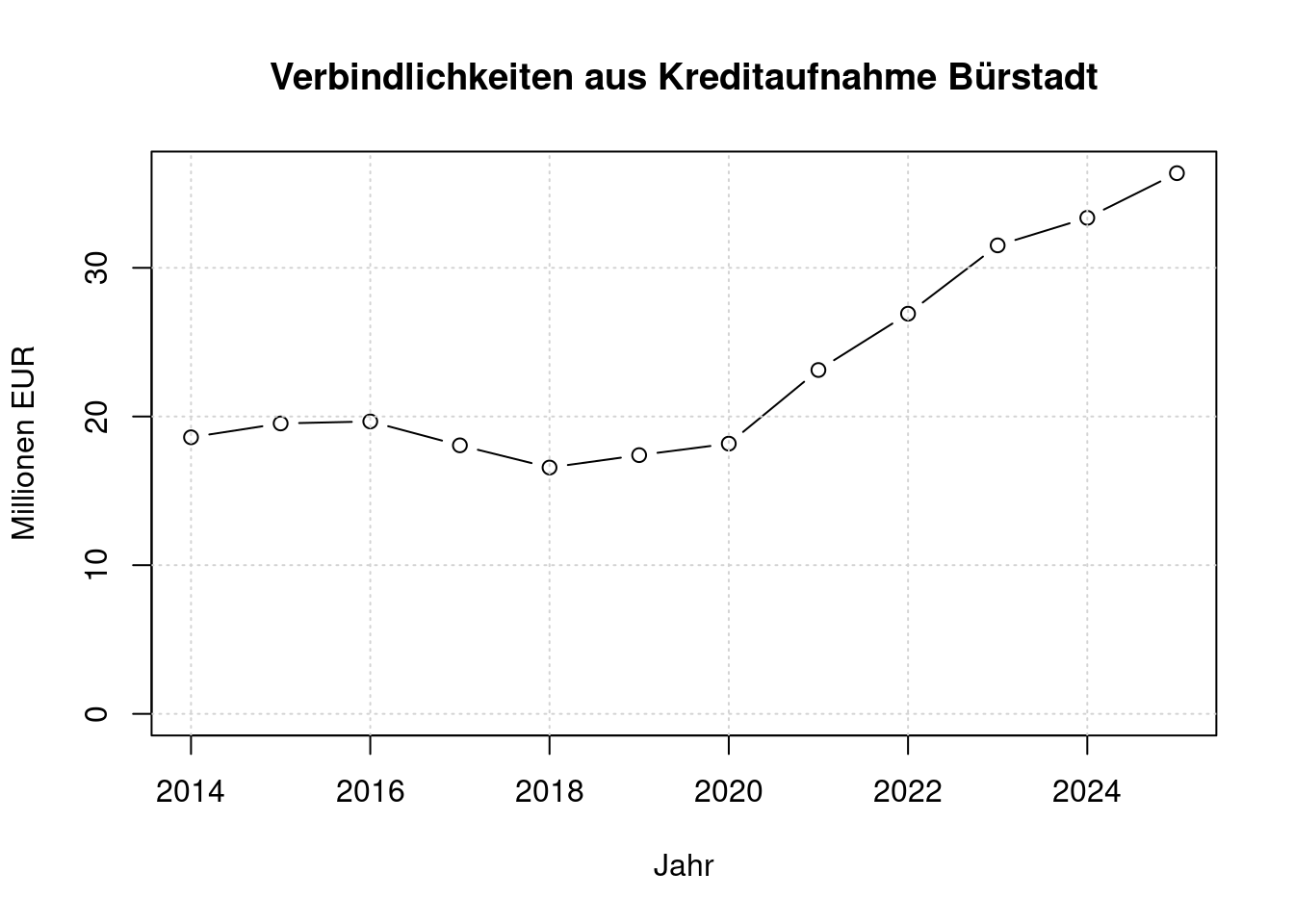
Ältere Jahre von https://statistik.hessen.de/sites/statistik.hessen.de/files/2023-08/lii7_j2022_schulden_tabelle_4a.xlsx Die Werte sind Endbestände des Angegebenen Jahres, wir tragen sie als Anfangsbestände des Folgejahres ein.
s <- read.table('statistik_hessen.csv', header=TRUE, sep="\t")
a <- d
a[nrow(a)+1,] = c(1997, s$X1996)
a[nrow(a)+1,] = c(1998, s$X1997)
a[nrow(a)+1,] = c(1999, s$X1998)
a[nrow(a)+1,] = c(2000, s$X1999)
a[nrow(a)+1,] = c(2001, s$X2000)
a[nrow(a)+1,] = c(2002, s$X2001)
a[nrow(a)+1,] = c(2003, s$X2002)
a[nrow(a)+1,] = c(2004, s$X2003)
a[nrow(a)+1,] = c(2005, s$X2004)
a[nrow(a)+1,] = c(2006, s$X2005)
a[nrow(a)+1,] = c(2007, s$X2006)
a[nrow(a)+1,] = c(2008, s$X2007)
a[nrow(a)+1,] = c(2009, s$X2008)
a[nrow(a)+1,] = c(2010, s$X2009)
a[nrow(a)+1,] = c(2011, s$X2010)
a[nrow(a)+1,] = c(2012, s$X2011)
a[nrow(a)+1,] = c(2013, s$X2012)
a <- a[order(a$jahr),]
knitr::kable(a);| jahr | anfangsbestand | |
|---|---|---|
| 13.1 | 1997 | 13377441 |
| 14 | 1998 | 12758266 |
| 15 | 1999 | 13490948 |
| 16 | 2000 | 12897338 |
| 17 | 2001 | 12322646 |
| 18 | 2002 | 13271603 |
| 19 | 2003 | 13497000 |
| 20 | 2004 | 13040000 |
| 21 | 2005 | 12513000 |
| 22 | 2006 | 13249000 |
| 23 | 2007 | 13951000 |
| 24 | 2008 | 15099000 |
| 25 | 2009 | 15407000 |
| 26 | 2010 | 17626000 |
| 27 | 2011 | 16894006 |
| 28 | 2012 | 15270761 |
| 29 | 2013 | 17518851 |
| 2 | 2014 | 18601538 |
| 3 | 2015 | 19532359 |
| 4 | 2016 | 19666126 |
| 5 | 2017 | 18059767 |
| 6 | 2018 | 16567977 |
| 7 | 2019 | 17400412 |
| 8 | 2020 | 18174247 |
| 9 | 2021 | 23125640 |
| 10 | 2022 | 26913000 |
| 11 | 2023 | 31508080 |
| 12 | 2024 | 33360080 |
| 13 | 2025 | 36364810 |
plot(a$jahr, a$anfangsbestand/(1000*1000), type='b', ylim=c(0, max(d$anfangsbestand)/(1000*1000)),
main='Verbindlichkeiten aus Kreditaufnahme Bürstadt',
xlab='Jahr', ylab='Millionen EUR')
grid();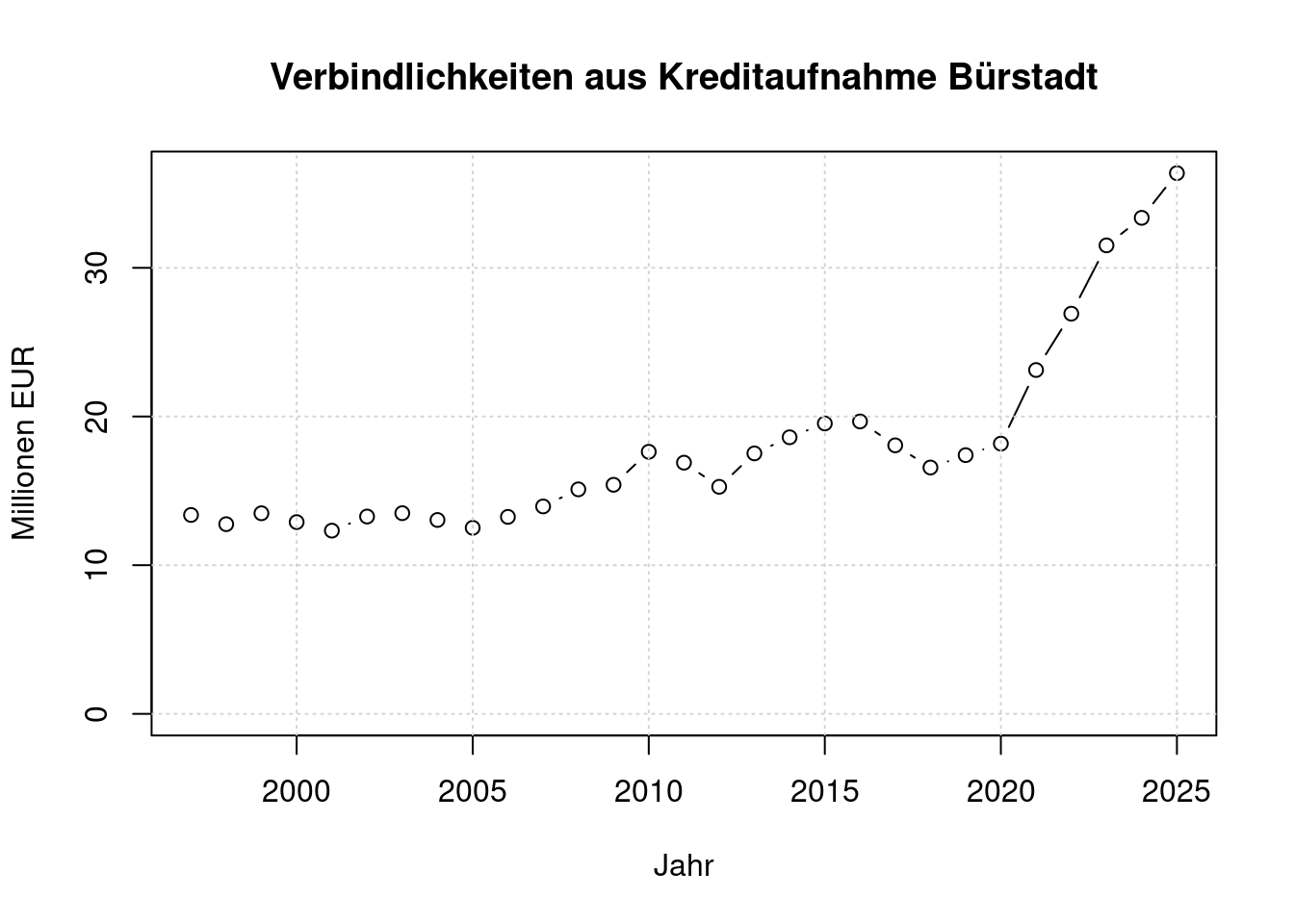
2.1 Inflationsbereinigung
https://www-genesis.destatis.de/datenbank/online/url/2f6c6113
Die Indexwerte geben den Index-Stand am Ende eines Jahres an. Der Wert für 2024 ist vom Oktober 2024.
inflation <- read.table('inflation.csv', header=TRUE, sep="\t")
inflation <- subset(inflation, jahr >= min(a$jahr)-1)
a$index <- inflation$index
a$bereinigt <- a$anfangsbestand * max(a$index)/a$index
knitr::kable(a, align='lcccc');| jahr | anfangsbestand | index | bereinigt | |
|---|---|---|---|---|
| 13.1 | 1997 | 13377441 | 72.0 | 22332894 |
| 14 | 1998 | 12758266 | 73.4 | 20892965 |
| 15 | 1999 | 13490948 | 74.0 | 21913674 |
| 16 | 2000 | 12897338 | 74.5 | 20808859 |
| 17 | 2001 | 12322646 | 75.5 | 19618305 |
| 18 | 2002 | 13271603 | 77.0 | 20717490 |
| 19 | 2003 | 13497000 | 78.1 | 20772592 |
| 20 | 2004 | 13040000 | 78.9 | 19865754 |
| 21 | 2005 | 12513000 | 80.2 | 18753898 |
| 22 | 2006 | 13249000 | 81.5 | 19540243 |
| 23 | 2007 | 13951000 | 82.8 | 20252539 |
| 24 | 2008 | 15099000 | 84.7 | 21427388 |
| 25 | 2009 | 15407000 | 86.9 | 21310948 |
| 26 | 2010 | 17626000 | 87.2 | 24296390 |
| 27 | 2011 | 16894006 | 88.1 | 23049484 |
| 28 | 2012 | 15270761 | 90.0 | 20394950 |
| 29 | 2013 | 17518851 | 91.7 | 22963641 |
| 2 | 2014 | 18601538 | 93.1 | 24016165 |
| 3 | 2015 | 19532359 | 94.0 | 24976485 |
| 4 | 2016 | 19666126 | 94.5 | 25014479 |
| 5 | 2017 | 18059767 | 95.0 | 22850358 |
| 6 | 2018 | 16567977 | 96.4 | 20658411 |
| 7 | 2019 | 17400412 | 98.1 | 21320383 |
| 8 | 2020 | 18174247 | 99.5 | 21955222 |
| 9 | 2021 | 23125640 | 100.0 | 27797019 |
| 10 | 2022 | 26913000 | 103.1 | 31376747 |
| 11 | 2023 | 31508080 | 110.2 | 34367252 |
| 12 | 2024 | 33360080 | 116.7 | 34360597 |
| 13 | 2025 | 36364810 | 120.2 | 36364810 |
plot(a$jahr, a$bereinigt/(1000*1000), type='b', ylim=c(0, max(d$anfangsbestand)/(1000*1000)),
main='Verbindlichkeiten aus Kreditaufnahme Bürstadt Inflationsbereinigt',
xlab='Jahr', ylab='Millionen EUR')
grid();
abline(v=2013.5, col='darkblue')
text(2013.5, 3, 'Bgm\nSchader', col='darkblue');
abline(v=2019.75, col='darkred')
text(2019.5, 3, 'Sport-\npark', col='darkred');
abline(v=2021.5, col='darkred')
text(2021.5, 8, 'Straßen-\nBeiträge', col='darkred');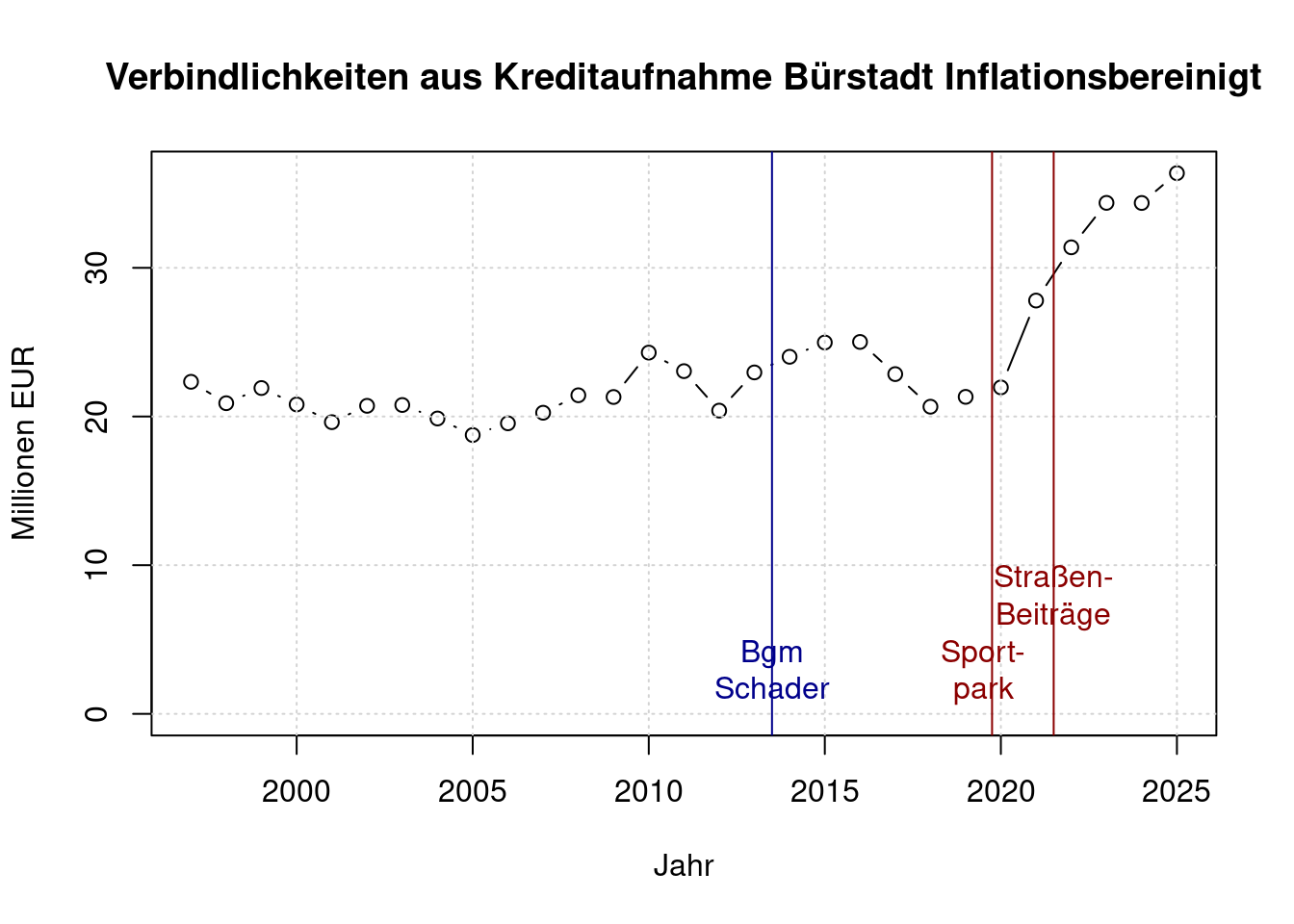
2.2 Trendberechnung vor / ab 2020
(trendb4 <- lm( bereinigt/(1000*1000)~jahr, subset(a, jahr <= 2020 ) ));##
## Call:
## lm(formula = bereinigt/(1000 * 1000) ~ jahr, data = subset(a,
## jahr <= 2020))
##
## Coefficients:
## (Intercept) jahr
## -198.4627 0.1096(trend2021 <- lm( bereinigt/(1000*1000)~jahr, subset(a, jahr >=2021 ) ));##
## Call:
## lm(formula = bereinigt/(1000 * 1000) ~ jahr, data = subset(a,
## jahr >= 2021))
##
## Coefficients:
## (Intercept) jahr
## -4037.308 2.012Seit 2021 machen wir im Mittel pro Jahr also 2 Millionen € neue Schulden.
ncitizen <- 16980;
per_year <- coef(trend2021)[2] * (1000*1000)
per_year / ncitizen;## jahr
## 118.489Pro Bürger*in und Jahr also Schulden von 120€
Zunahme der Kommunalen Schulden seit 2020 von 69%:
max(a$bereinigt) / mean(subset(a, jahr <=2020)$bereinigt)## [1] 1.6793332.3 Mit Straßenbeiträgen
Wenn Bürstadt 2021 die Straßenbeiträge nicht zurückgezahlt hätte, und dann dieselben Straßenbaumaßnahmen durchgeführt hätte, dann wären die zurückgezahlten Straßenbeiträge noch auf dem Konto, und jedes Jahr seither wären 1,23 Millionen € an Straßenbeiträgen eingegangen. Daneben wären entsprechend weniger Zinsen und Zinsenszinsen angefallen.
4,91 Millionen € wurden 2021 zurückgezahlt. 1,18 Millionen € für 2018 hätte Bürstadt wohl zurückzahlen müssen, weil von der Verwaltung ein Formfehler gemacht wurde.
# stb: Straßenbeiträge in Millionen €
a$stb <- rep( 0, nrow(a) )
a$stb[ 2022-a$jahr[1]+1 ] <- (4.91 - 1.18);
a$stb[ 2023-a$jahr[1]+1 ] <- 1.23;
a$stb[ 2024-a$jahr[1]+1 ] <- 1.23;
a$stb[ 2025-a$jahr[1]+1 ] <- 1.23;
# Zinsen 2%
interest <- 1.02;
# Zinsen berücksichtigen
a$stb[ 2022-a$jahr[1]+1 ] <- a$stb[ 2022-a$jahr[1]+1 ] * interest ^ (2024-2021);
a$stb[ 2023-a$jahr[1]+1 ] <- a$stb[ 2023-a$jahr[1]+1 ] * interest ^ (2024-2022);
a$stb[ 2024-a$jahr[1]+1 ] <- a$stb[ 2024-a$jahr[1]+1 ] * interest ^ (2024-2023);
a$stb[ 2025-a$jahr[1]+1 ] <- a$stb[ 2025-a$jahr[1]+1 ] * interest ^ (2024-2024);
# Addieren
a$stbsum <- a$stb;
i <- 2;
while (i<=nrow(a))
{
a$stbsum[i] <- a$stbsum[i] + a$stbsum[i-1];
i <- i+1;
}
# Von Schuldenstand abziehen
a$anfangsbestandstb <- a$anfangsbestand - a$stbsum*(1000*1000);
# Inflationskorrektur
a$bereinigtstb <- a$anfangsbestandstb * max(a$index)/a$index
knitr::kable(a);| jahr | anfangsbestand | index | bereinigt | stb | stbsum | anfangsbestandstb | bereinigtstb | |
|---|---|---|---|---|---|---|---|---|
| 13.1 | 1997 | 13377441 | 72.0 | 22332894 | 0.000000 | 0.000000 | 13377441 | 22332894 |
| 14 | 1998 | 12758266 | 73.4 | 20892965 | 0.000000 | 0.000000 | 12758266 | 20892965 |
| 15 | 1999 | 13490948 | 74.0 | 21913674 | 0.000000 | 0.000000 | 13490948 | 21913674 |
| 16 | 2000 | 12897338 | 74.5 | 20808859 | 0.000000 | 0.000000 | 12897338 | 20808859 |
| 17 | 2001 | 12322646 | 75.5 | 19618305 | 0.000000 | 0.000000 | 12322646 | 19618305 |
| 18 | 2002 | 13271603 | 77.0 | 20717490 | 0.000000 | 0.000000 | 13271603 | 20717490 |
| 19 | 2003 | 13497000 | 78.1 | 20772592 | 0.000000 | 0.000000 | 13497000 | 20772592 |
| 20 | 2004 | 13040000 | 78.9 | 19865754 | 0.000000 | 0.000000 | 13040000 | 19865754 |
| 21 | 2005 | 12513000 | 80.2 | 18753898 | 0.000000 | 0.000000 | 12513000 | 18753898 |
| 22 | 2006 | 13249000 | 81.5 | 19540243 | 0.000000 | 0.000000 | 13249000 | 19540243 |
| 23 | 2007 | 13951000 | 82.8 | 20252539 | 0.000000 | 0.000000 | 13951000 | 20252539 |
| 24 | 2008 | 15099000 | 84.7 | 21427388 | 0.000000 | 0.000000 | 15099000 | 21427388 |
| 25 | 2009 | 15407000 | 86.9 | 21310948 | 0.000000 | 0.000000 | 15407000 | 21310948 |
| 26 | 2010 | 17626000 | 87.2 | 24296390 | 0.000000 | 0.000000 | 17626000 | 24296390 |
| 27 | 2011 | 16894006 | 88.1 | 23049484 | 0.000000 | 0.000000 | 16894006 | 23049484 |
| 28 | 2012 | 15270761 | 90.0 | 20394950 | 0.000000 | 0.000000 | 15270761 | 20394950 |
| 29 | 2013 | 17518851 | 91.7 | 22963641 | 0.000000 | 0.000000 | 17518851 | 22963641 |
| 2 | 2014 | 18601538 | 93.1 | 24016165 | 0.000000 | 0.000000 | 18601538 | 24016165 |
| 3 | 2015 | 19532359 | 94.0 | 24976485 | 0.000000 | 0.000000 | 19532359 | 24976485 |
| 4 | 2016 | 19666126 | 94.5 | 25014479 | 0.000000 | 0.000000 | 19666126 | 25014479 |
| 5 | 2017 | 18059767 | 95.0 | 22850358 | 0.000000 | 0.000000 | 18059767 | 22850358 |
| 6 | 2018 | 16567977 | 96.4 | 20658411 | 0.000000 | 0.000000 | 16567977 | 20658411 |
| 7 | 2019 | 17400412 | 98.1 | 21320383 | 0.000000 | 0.000000 | 17400412 | 21320383 |
| 8 | 2020 | 18174247 | 99.5 | 21955222 | 0.000000 | 0.000000 | 18174247 | 21955222 |
| 9 | 2021 | 23125640 | 100.0 | 27797019 | 0.000000 | 0.000000 | 23125640 | 27797019 |
| 10 | 2022 | 26913000 | 103.1 | 31376747 | 3.958306 | 3.958306 | 22954694 | 26761923 |
| 11 | 2023 | 31508080 | 110.2 | 34367252 | 1.279692 | 5.237998 | 26270082 | 28653937 |
| 12 | 2024 | 33360080 | 116.7 | 34360597 | 1.254600 | 6.492598 | 26867482 | 27673276 |
| 13 | 2025 | 36364810 | 120.2 | 36364810 | 1.230000 | 7.722598 | 28642212 | 28642212 |
plot(a$jahr, a$bereinigt/(1000*1000), type='b', ylim=c(0, max(d$anfangsbestand)/(1000*1000)),
main='Verbindlichkeiten Bürstadt mit Straßenbeiträgen',
xlab='Jahr', ylab='Millionen EUR')
grid();
lines(a$jahr, a$bereinigtstb/(1000*1000), col='darkgreen', type='b', lwd=3);
abline(v=2013.5, col='darkblue')
text(2013.5, 3, 'Bgm\nSchader', col='darkblue');
abline(v=2019.75, col='darkred')
text(2019.5, 3, 'Sport-\npark', col='darkred');
abline(v=2021.5, col='darkred')
text(2021.5, 8, 'Straßen-\nBeiträge', col='darkred');
lines(2021:2025, predict(trend2021), col='darkred');
lines(1997:2020, predict(trendb4), col='green')
legend(x= "bottomleft",
legend=c("Tatsächliche Schulden", "Schulden mit Straßenbeiträgen", "Trend ab 2021", "Trend bis 2020"),
col=c("black", "darkgreen", "darkred", "green"),
lwd=c(1, 3, 1, 1));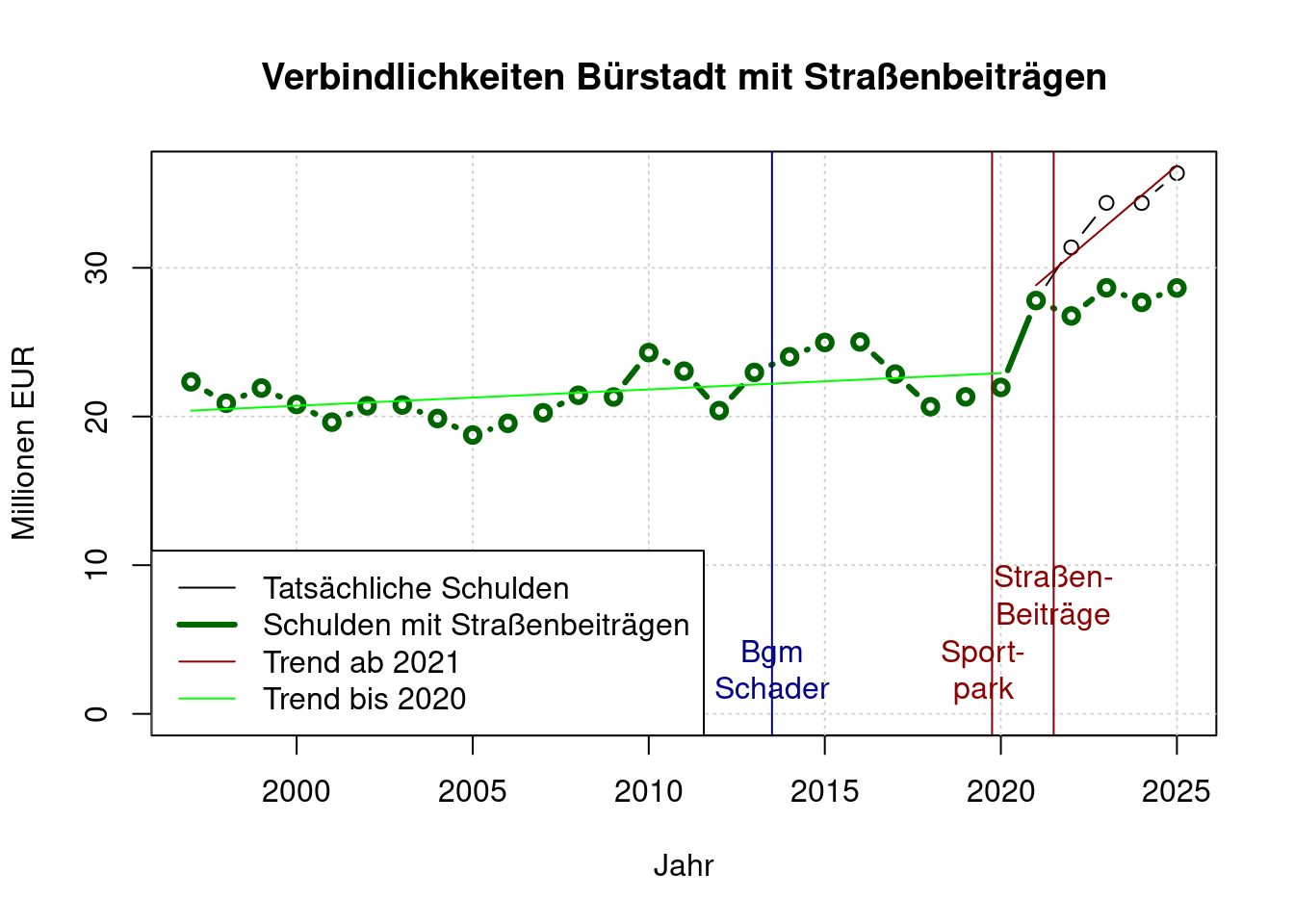
2.4 Trend mit Straßenbeiträgen
(trendstb <- lm( bereinigtstb/(1000*1000)~jahr, subset(a, jahr >=2021 ) ));##
## Call:
## lm(formula = bereinigtstb/(1000 * 1000) ~ jahr, data = subset(a,
## jahr >= 2021))
##
## Coefficients:
## (Intercept) jahr
## -498.4262 0.2602Wenn wir die Straßenbeiträge also nicht abgeschafft hätten, dann hätten wir statt 2 Millionen € im Jahr stattdessen nur 0,3 Millionen € neue Schulden gemacht.
3 Anhebung Grundsteuer B
Laut Beschlussvorlage XIX/KA/0009 Bewirkt eine Hebesatzerhöhung der Grundsteuer B um 10% Mehreinnahmen von 54.000 €.
Um die für Straßenbeiträge durchschnittlich pro Jahr entfallenen 1,23 Millionen € aus der Grundsteuer B zu beziehen, müsste diese also angepasst werden um:
1.23e6 * 10 / 54000;## [1] 227.7778Lt Beschlussvorlage XIX/Fa/0097 beträgt der Hebesatz der Grundsteuer B nun 570 %. Also von 570 % auf
1.23e6 * 10 / 54000 + 570;## [1] 797.77784 Vergleich mit anderen Kommunen
Kreditaufnahme je Bürger*in:
a$anfangsbestand[nrow(a)] / ncitizen## [1] 2141.626Lt. https://www.n-tv.de/regionales/hessen/Verschuldung-hessischer-Kommunen-weiter-ueber-Bundesschnitt-article24123240.html waren es in Hessen im Mittel 2420€ / Person und deutschlandweit 1800€ / Person. Demnach liegt Bürstadt noch unter dem hessischen Durchschnitt, aber deutlich über dem Bundesdurchschnitt.
5 Vergleich mit Haushaltsvolumen
Bürstadts Einkünfte sind in den letzten Jahren etwas mehr als die Inflation angestiegen. Das lag hauptsächlich an der intensiven Entwicklung neuer Gewerbeflächen, die zu höheren Gewerbesteuereinnahmen führten. Dabei hat Bürstadt die empfohlenen Richtwerte zum Flächenverbrauch der Bundesregierung und der UN nicht erfüllt. Bürstadt hat dafür eine Genehmigung beantragt.
Steigerungen in der Wirtschaftsleistung sind auch mit Steigerungen in den CO2-Emissionen verknüpft. Wirtschaftswachstum ohne Energiewende und Artenschutz bedeutet eine Steigerung in der Geschwindigkeit der Umweltzerstörung. Um diese Steigerung zu kompensieren, wären zusätzliche Anstrengungen im Klima- und Artenschutz über die ohnehin noch nie erreichten Anstregungen hinaus, wie sie ohne Wirtschaftswachstum notwendig wären, erforderlich.
Gewerbesteuereinnahmen haben eine Tendenz zu starken Schwankungen, weil sie stark von der konjunkturellen Lage abhängen und sehr schnell einbrechen können. Die Verpflichtungen zur Schuldentilgung und Zinszahlung bestehen dann aber fort.
Gesamtbetrag der Erträge lt. Haushaltsplänen der Jahre 2017 bis 2024.
e <- subset(data.frame(jahr=a$jahr, anfangsbestand=a$anfangsbestand), jahr >= 2015 & jahr <= 2024);
e$ertraege <- c(27165219,30629531,34465444,37581943,38237165,40319027,40109318,43210769,47069985,50318445);
e$prz_verschuldung <- e$anfangsbestand / e$ertraege * 100;
knitr::kable(e);| jahr | anfangsbestand | ertraege | prz_verschuldung | |
|---|---|---|---|---|
| 19 | 2015 | 19532359 | 27165219 | 71.90209 |
| 20 | 2016 | 19666126 | 30629531 | 64.20642 |
| 21 | 2017 | 18059767 | 34465444 | 52.39964 |
| 22 | 2018 | 16567977 | 37581943 | 44.08494 |
| 23 | 2019 | 17400412 | 38237165 | 45.50654 |
| 24 | 2020 | 18174247 | 40319027 | 45.07611 |
| 25 | 2021 | 23125640 | 40109318 | 57.65653 |
| 26 | 2022 | 26913000 | 43210769 | 62.28308 |
| 27 | 2023 | 31508080 | 47069985 | 66.93879 |
| 28 | 2024 | 33360080 | 50318445 | 66.29792 |
plot(e$jahr, e$ertraege/(1000*1000), type='b', ylim=c(0, max(e$ertraege)/(1000*1000)),
main='Entwicklung des Jahresertrags',
xlab='Jahr', ylab='Millionen EUR',
col='darkgreen', lwd=3)
lines(e$jahr, e$anfangsbestand/(1000*1000), type='b', col='darkred');
grid();
legend(x= "bottomright",
legend=c("Jahresertrag", "Schulden"),
col=c("darkgreen", "darkred"),
lwd=c(3, 1));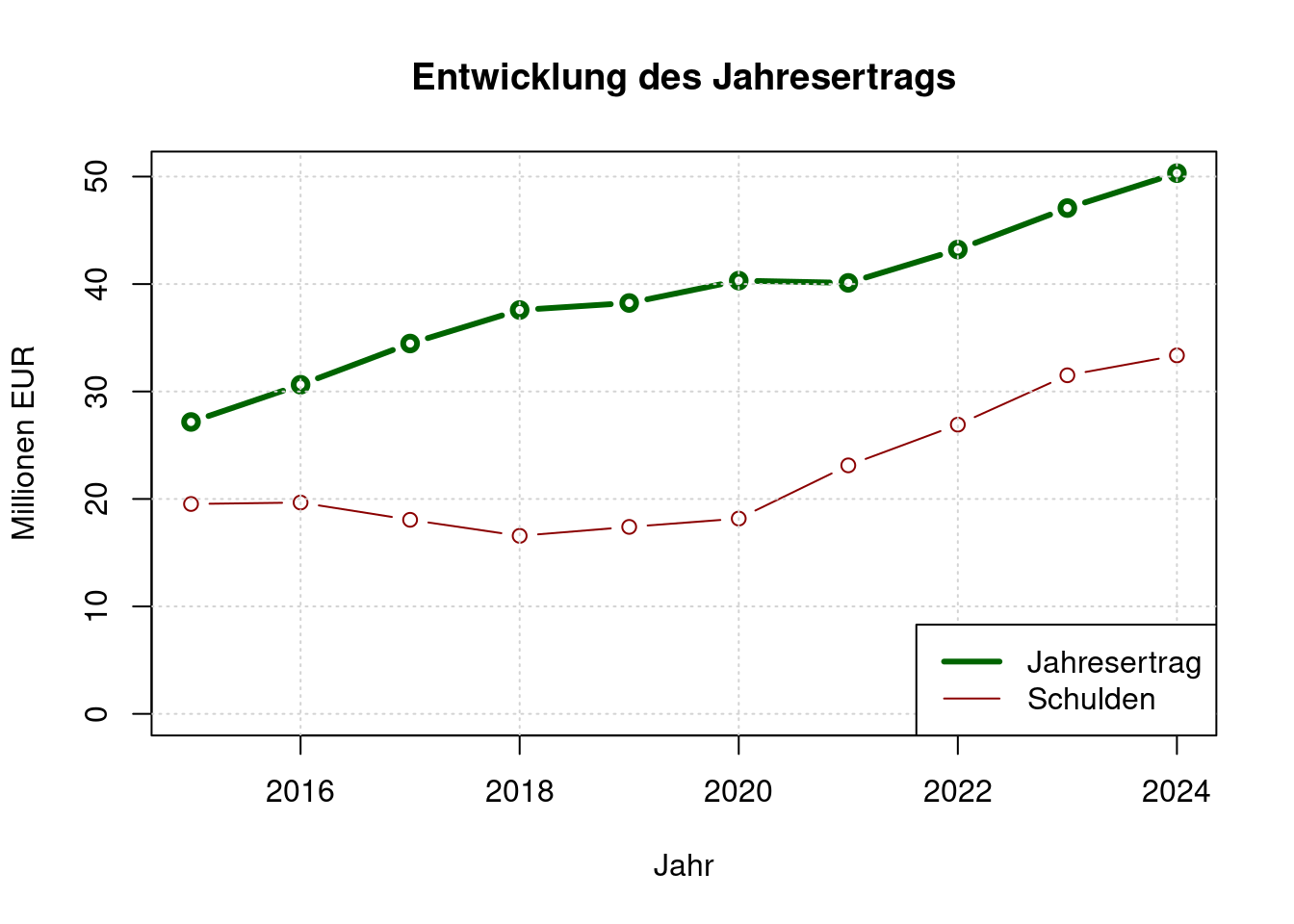
plot(e$jahr, e$prz_verschuldung, type='b',
main='Verschuldung in % des Jahresertrags',
xlab='Jahr', ylab='% Verschuldung')
grid();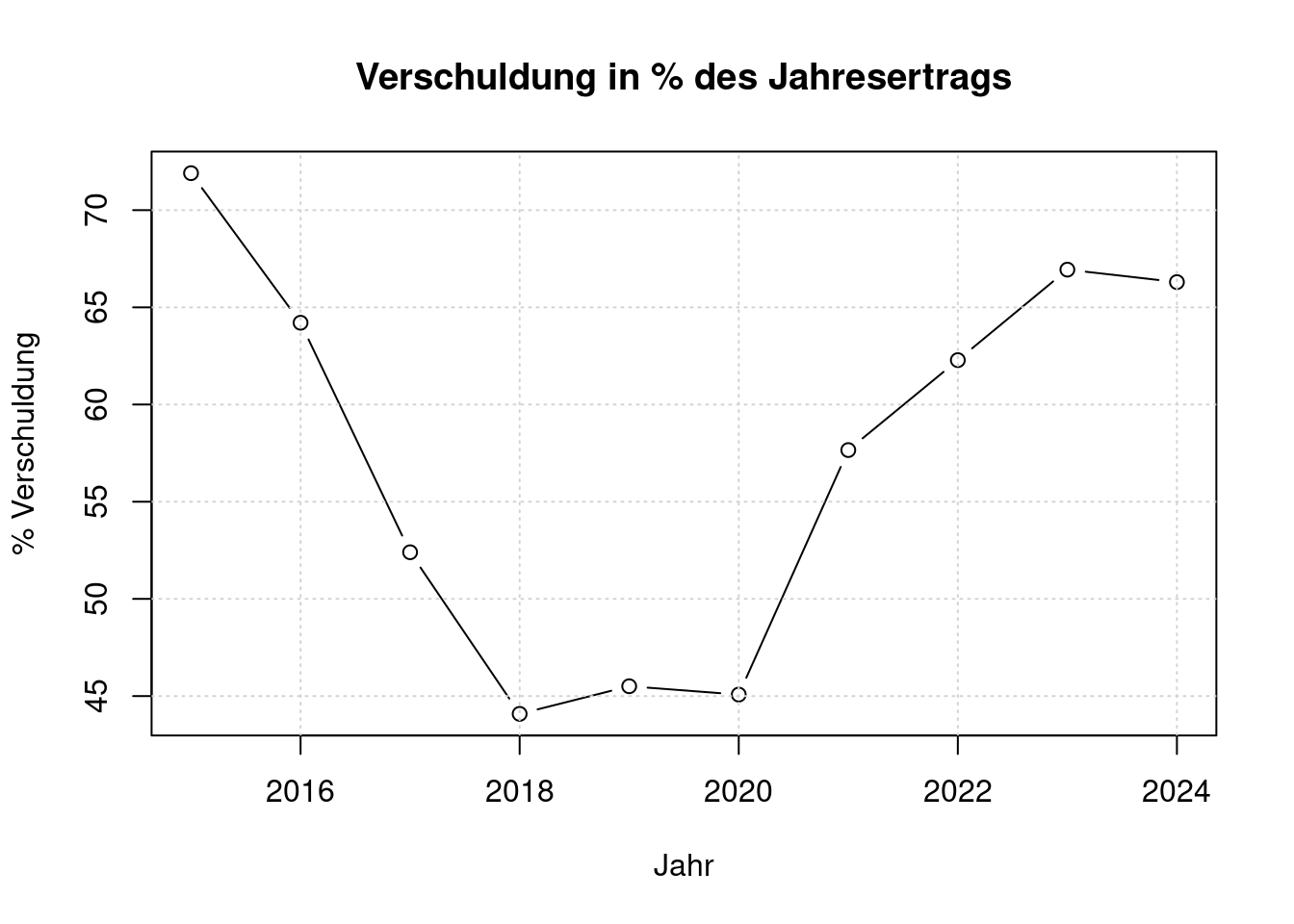
schuldenaufnahme <- e$anfangsbestand[2:nrow(e)] - e$anfangsbestand[1:(nrow(e))-1]
plot(e$jahr[2:nrow(e)], schuldenaufnahme/(1000*1000), type='b',
main='Aufnahme neuer Schulden',
xlab='Jahr', ylab='Millionen EUR');
grid();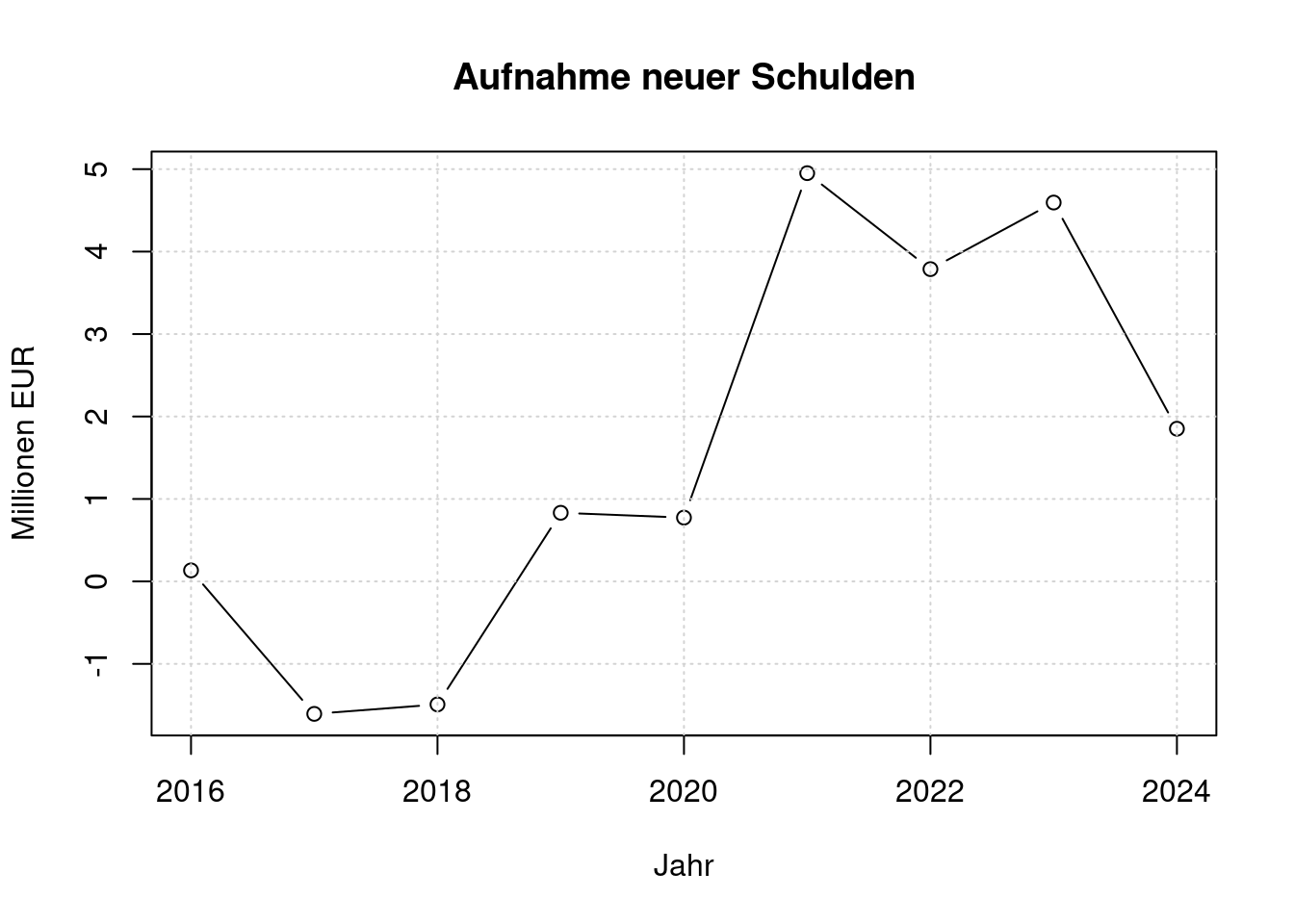
plot(e$jahr[2:nrow(e)], schuldenaufnahme/e$ertraege[2:nrow(e)]*100, type='b',
main='Aufnahme neuer Schulden in % des Jahresertrags',
xlab='Jahr', ylab='% Schuldenaufnahme')
grid();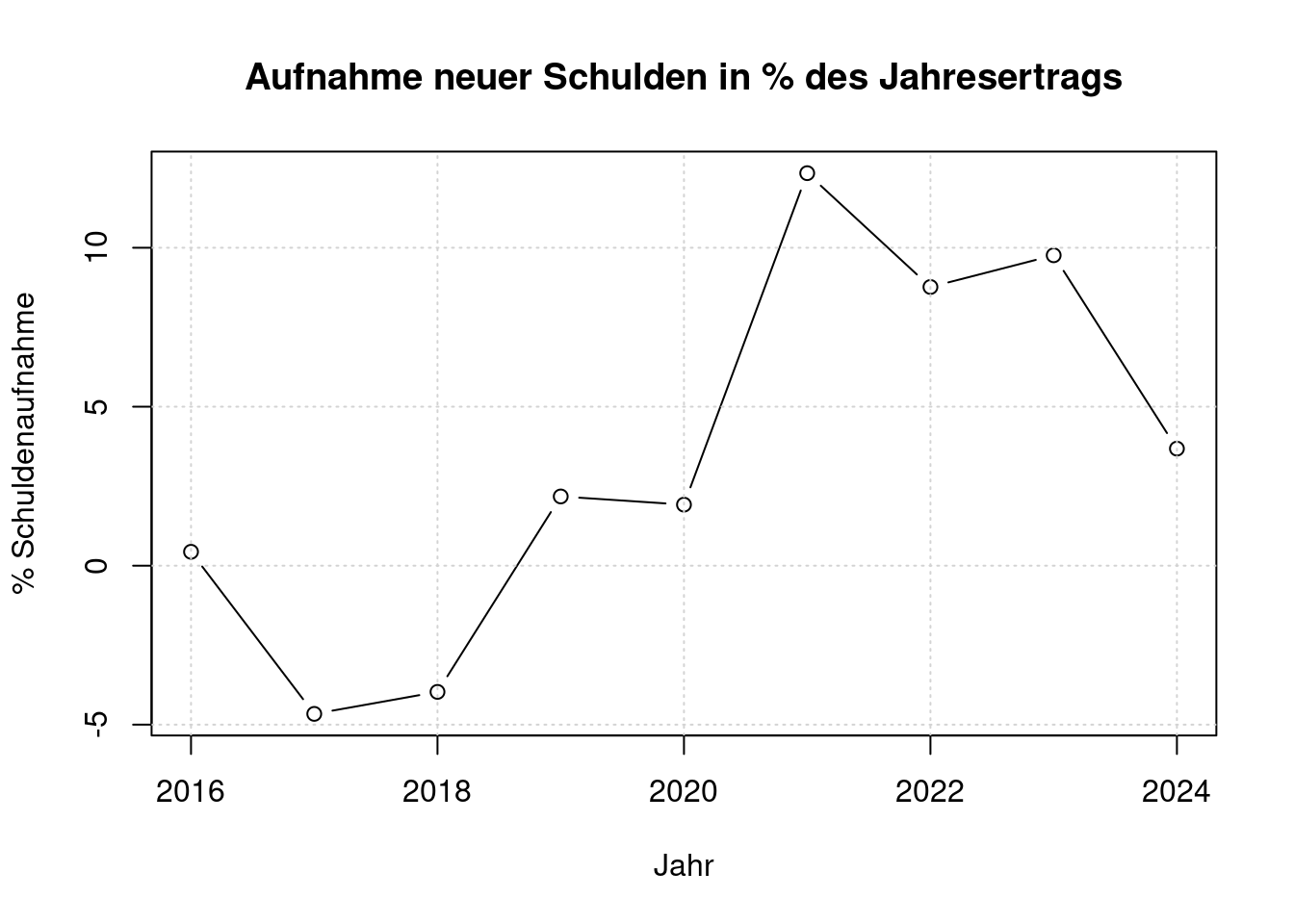
5.1 Entwicklung der Steuereinnahmen
Quelle: https://www.buerstadt.de/fileadmin/Dateien/Cross7/Root/de/Rathaus_%26_Politik/Rathausservice/Haushaltsplan/Entwurf_Haushalt_2024.pdf Seite 32.
e$gewerbesteuer<-c( 4004442, 4703185, 4080727, 4274058, 4802996, 5886046, 7592562, 6776600, 7200000, 9000000);
e$grundsteuer <-c( 2039085, 2089012, 2094535, 2123446, 2045851, 2446699, 2769033, 2617431, 2782000, 3222000);
e$gemeinschaft <-c( 8803772, 9263899, 9675997, 9888173,10564979,10171438,11410692,11382637,12780581,12927640);
e$schluesselz <-c( 4618749, 7384959, 7714853, 8190816, 9286607, 9302501, 9479920, 8586969, 9945291, 9710144);
e$steuersumme <-c(19466048,23441055,23566112,24476493,26700433,27806684,31252207,29363637,32707872,34859784);
library(lattice);
xyplot(schluesselz/1e6+gewerbesteuer/1e6+steuersumme/1e6+grundsteuer/1e6+gemeinschaft/1e6~jahr,
e, type=c('b','g'), auto.key=TRUE,
main="Entwicklung der Steuereinnahmen",
ylab="Millionen €");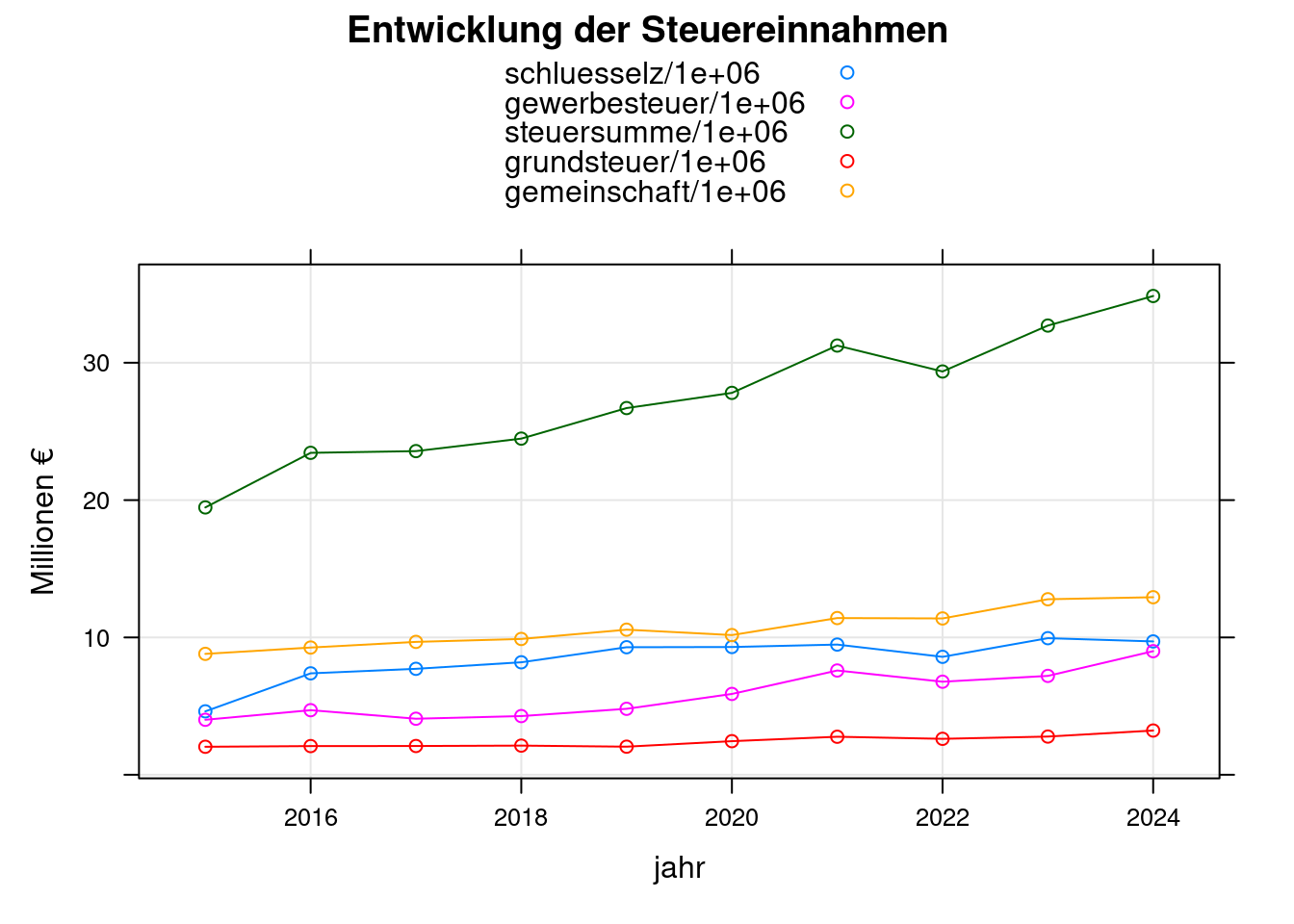
5.2 Inflationskorrektur für Steuereinnamen
e$index <- subset(inflation, jahr >= 2015)$index
e$gewerbesteuer <- e$gewerbesteuer * max(e$index)/e$index
e$grundsteuer <- e$grundsteuer * max(e$index)/e$index
e$gemeinschaft <- e$gemeinschaft * max(e$index)/e$index
e$schluesselz <- e$schluesselz * max(e$index)/e$index
e$steuersumme <- e$steuersumme * max(e$index)/e$index
xyplot(schluesselz/1e6+gewerbesteuer/1e6+steuersumme/1e6+grundsteuer/1e6+gemeinschaft/1e6~jahr,
e, type=c('b','g'), auto.key=TRUE,
main="Entwicklung der Steuereinnahmen inflationskorrigiert",
ylab="Millionen €");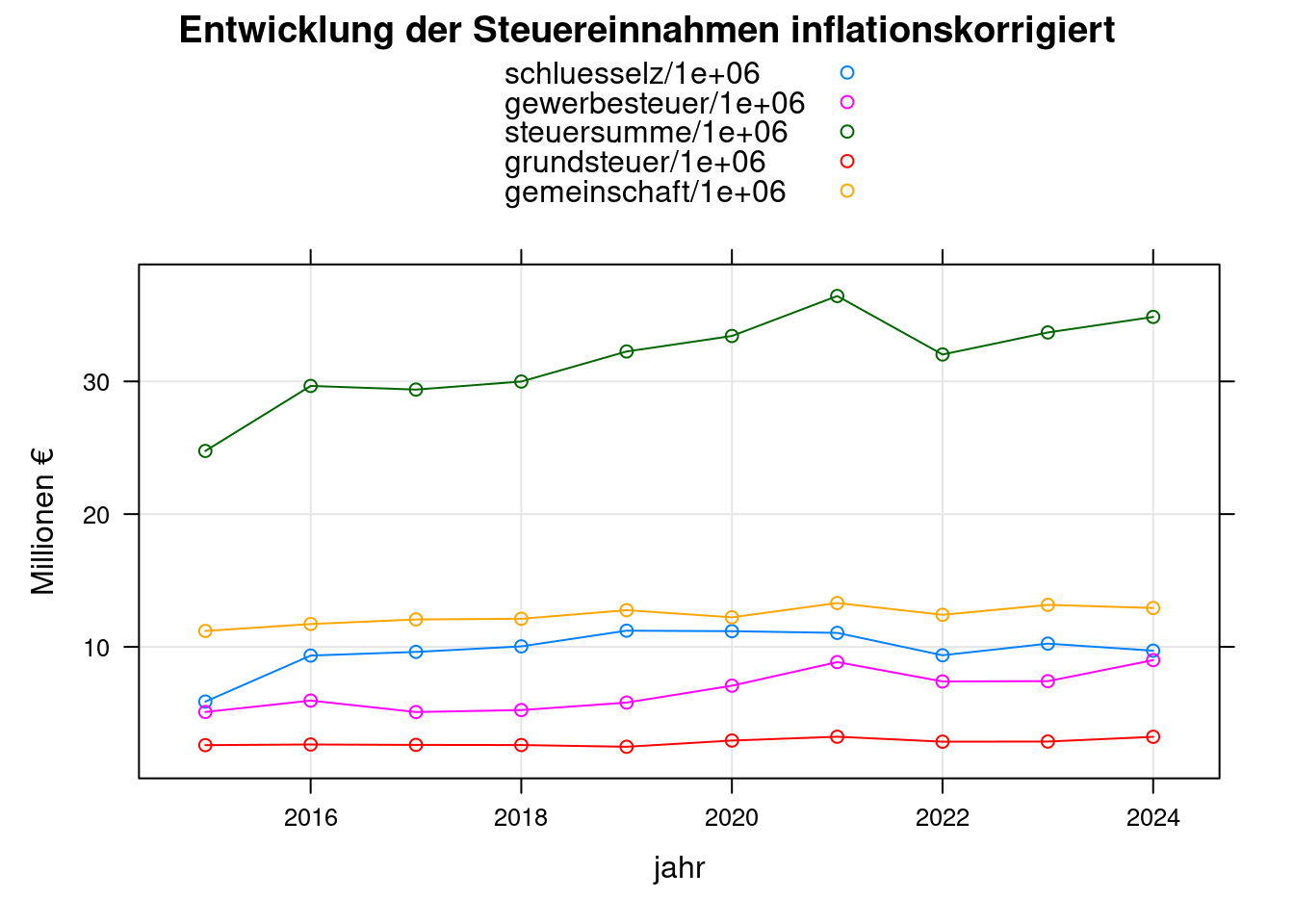
5.3 Übersicht nach Steuerarten
Schlüsselzuweisungen
sind Gelder aus dem Kommunalen Finanzausgleich KFA vom Land Hessen.
Dieser ist für alle Kommunen in Hesssen zusammen von 2010 2,95
Milliarden € auf 2024 7,13 Milliarden € gestiegen.  .
.
Gemeinschaftssteuern sind Anteile an Einkommens-, Körperschafts- und Umsatzsteuer.
Grundsteuer ist eine Steuer auf das Eigentum an Grundstücken und deren Bebauung. Die Gemeinde legt einen Hebesatz in % eines nominalen Werts fest. Die Berechnungsmethode der Grundsteuer berücksichtigt nicht die Inflation. Dementsprechend müsste der Grundsteuer-Hebesatz bis 2024 in etwa der Inflation nachgefügert werden. Berechnungsgrundlage
Gewerbesteuer ist eine Steuer auf die Gewinne von Unternehmen. Die Gemeinde legt einen Hebesatz in % eines nominalen Werts fest. Die Gewinne von Unternehmen passen sich tendenziell der Inflation an, daher muss der Hebesatz nicht von der Gemeinde der Inflation angepasst werden.
library(ggplot2)
s <- rbind(data.frame(jahr=e$jahr, mio=e$gewerbesteuer/1e6, type='1Gewerbesteuer'),
data.frame(jahr=e$jahr, mio=e$grundsteuer/1e6, type='2Grundsteuer'),
data.frame(jahr=e$jahr, mio=e$schluesselz/1e6, type='3Schluesselz'),
data.frame(jahr=e$jahr, mio=e$gemeinschaft/1e6, type='4Gemeinschaft'));
ggplot(s, aes(fill=type, y=mio, x=jahr)) + geom_col() +
scale_x_continuous(breaks=c(2015,2019,2021,2024)) +
labs(y = 'Millionen €') +
ggtitle('Entwicklung der Steuerarten Bürstadt inflationskorrigiert')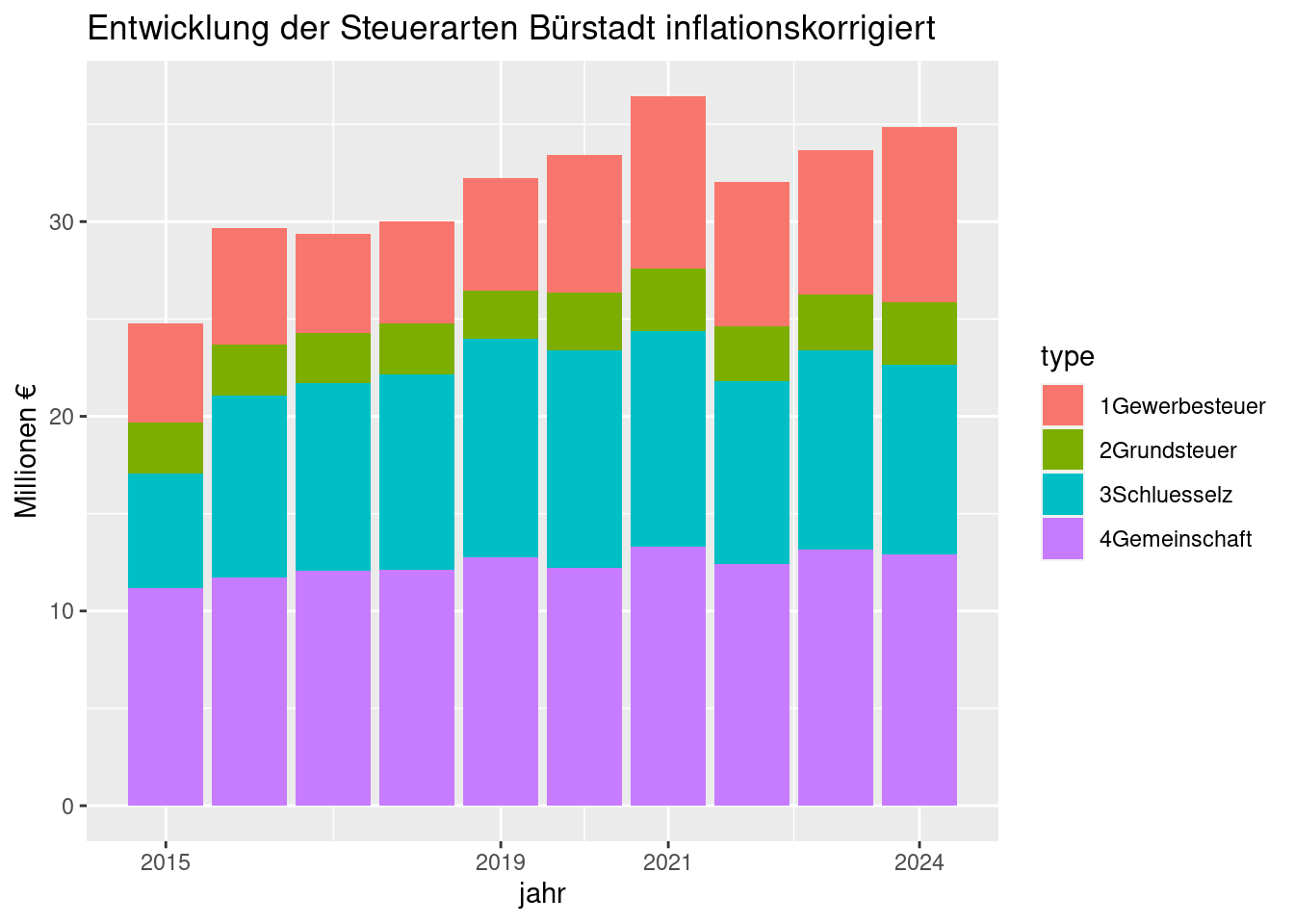
xyplot(schluesselz/e$schluesselz[nrow(e)]*100+
gewerbesteuer/e$gewerbesteuer[nrow(e)]*100+
grundsteuer/e$grundsteuer[nrow(e)]*100+
gemeinschaft/e$gemeinschaft[nrow(e)]*100~jahr,
e, type=c('b','g'), auto.key=TRUE,
main="Entwicklung der Steuerarten 2024=100",
ylab="% von 2024");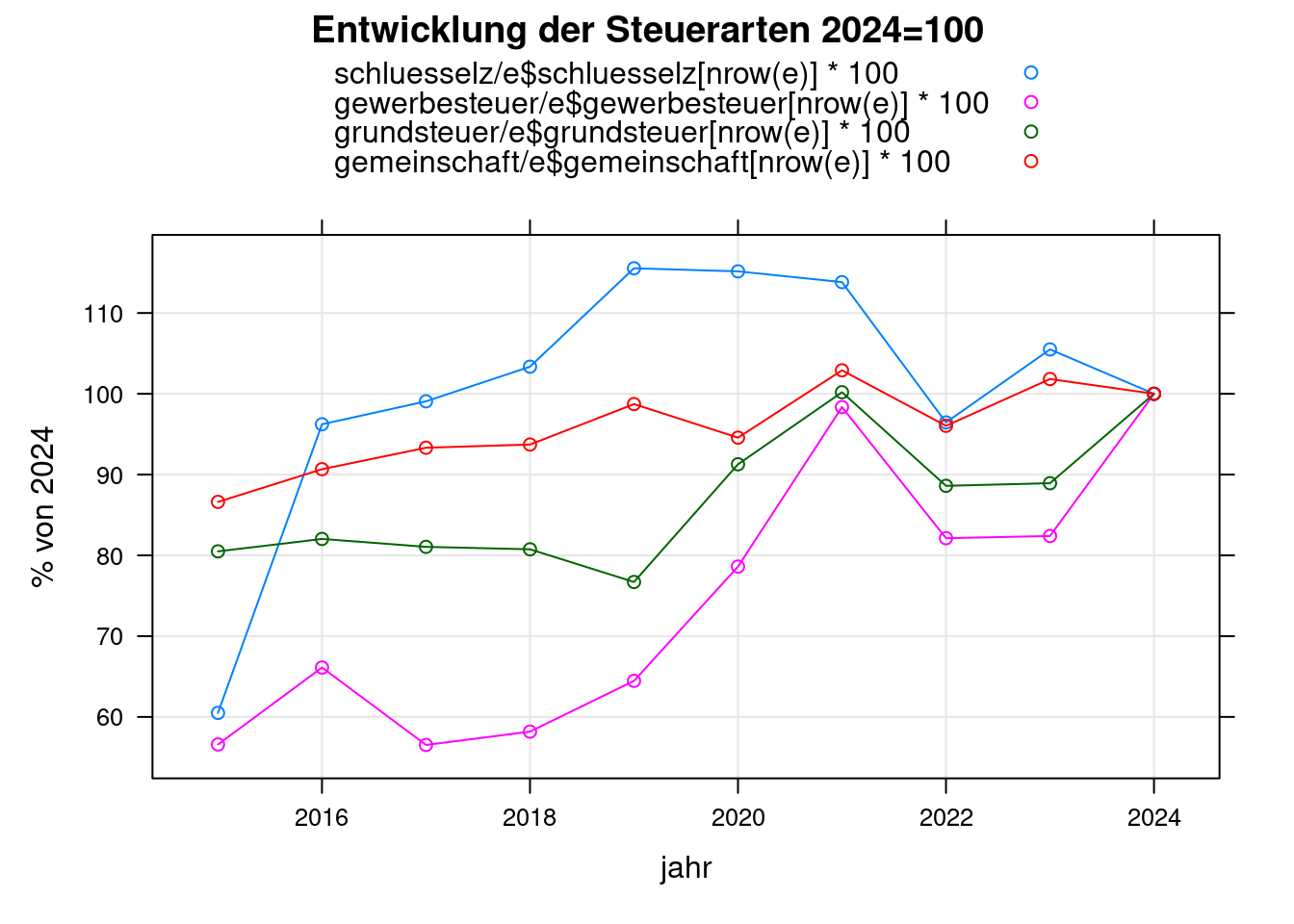
6 Grundsteuer
Entwicklung der Hebesätze:
h <- data.frame(
jahr = c(2004, 2005, 2006, 2007, 2010,2013,2014,2015,2016,2017,2018,2019,2020,2021,2022,2023,2024),
h_grundsteuera = c(NA , NA , NA , NA , NA ,NA ,NA ,NA ,350, 350, 350, 350, 370, 370, 370, 370, 370),
h_grundsteuerb = c(220 , 220 , 230 , 230 , 250 ,300 ,330 ,430 ,430, 430, 430, 430, 490, 490, 490, 490, 570),
h_gewerbesteuer= c(NA , NA , NA , NA , NA ,NA ,NA ,NA ,NA , 360, 360, 360, 380, 380, 380, 380, 380));
e <- merge(e, h);Die Grundsteuer für eine Grundstück berechnet sich aus dem Einheitswert multipliziert mit der Steueremesszahl und dem von der Gemeinde festgelegten Grundsteuer-Hebesatz.
Einheitswerte für Grundstücke wurden 1964 zuletzt festgestellt und seither nicht neu bewertet. Der einzige Faktor bei der Berechnung der Grundsteuer, der die Geldentwertung berücksichtigt, war damit bis 2024 die Grundsteuer-Hebesatz. Dieses Verfahren wurde vom Bundesverfassungsgericht als verfassungswidrig abgelehnt und wird daher ab 2025 durch ein neues Verfahren abgelöst.
6.1 Inflationsanpassung Grundsteuer-Hebesätze
6.1.1 Grundsteuer A
Grundsteuer A ist agraisch für Betriebe der Land- und Forstwirtschaft. Der Grundsteuer A hebesatz liegt 2024 in Bürstadt deutlich unter dem Kreis-Durchschnitt. Grundsteuer A sind 2,5 % des Grundsteueraufkommens in Bürstadt.
Für 2025 empfiehlt das Finanzamt, den Grundsteuer-Hebesatz A um 100 % anzuheben, damit die Einnahmen gleich bleiben.
Wenn der Grundsteuer A-Hebesatz seit 2016 regelmäßig nur der Inflation (Verbraucherpreisindex) angepasst worden wären, dann betrügen sie nun:
e$i_grundsteuera <- e$h_grundsteuera[2] * e$index / e$index[2];
plot(e$jahr, e$i_grundsteuera, type='b',
main='Grundsteuer A Hebesatz',
xlab='Jahr', ylab='%',
col='darkgreen', lwd=3);
lines(e$jahr, e$h_grundsteuera, type='b');
grid();
legend(x= "topleft",
legend=c("Hebesatz entsprechend Inflationskorrektur ab 2016", "Tatsächlicher Hebesatz"),
col=c("darkgreen", "black"),
lwd=c(3, 1));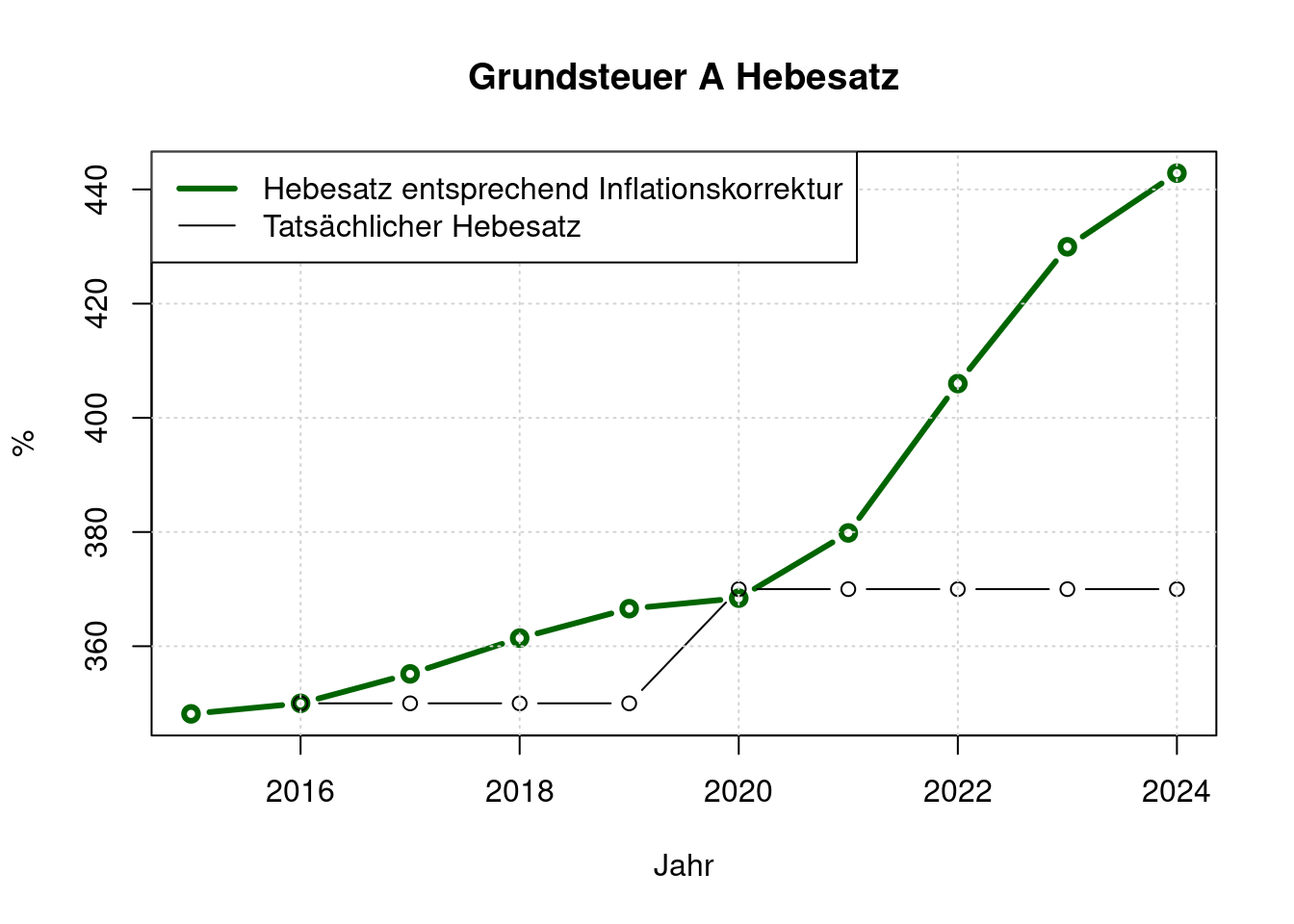
6.1.2 Grundsteuer B
Grundsteuer B ist baulich für bebaute oder unbebaute Grundstücke.
Für 2025 sagt das Finanzamt, dass die Grundsteuer B um 100 % gesenkt werden müsste, damit die Einnahmen gleich blieben. Beibehalten des derzeitigen Hebesatzes entspräche also einer Erhöhung von 100 % nach dem alten Verfahren.
Wenn der Grundsteuer B-Hebesatz seit 2016 regelmäßig nur der Inflation (Verbraucherpreisindex) angepasst worden wären, dann betrügen sie nun:
e$i_grundsteuerb <- e$h_grundsteuerb[2] * e$index / e$index[2];
plot(e$jahr, e$i_grundsteuerb, type='b',
main='Grundsteuer B Hebesatz',
xlab='Jahr', ylab='%',
col='darkgreen', lwd=3,
ylim=c(430,570));
lines(e$jahr, e$h_grundsteuerb, type='b');
grid();
legend(x= "topleft",
legend=c("Hebesatz entsprechend Inflationskorrektur ab 2016", "Tatsächlicher Hebesatz"),
col=c("darkgreen", "black"),
lwd=c(3, 1));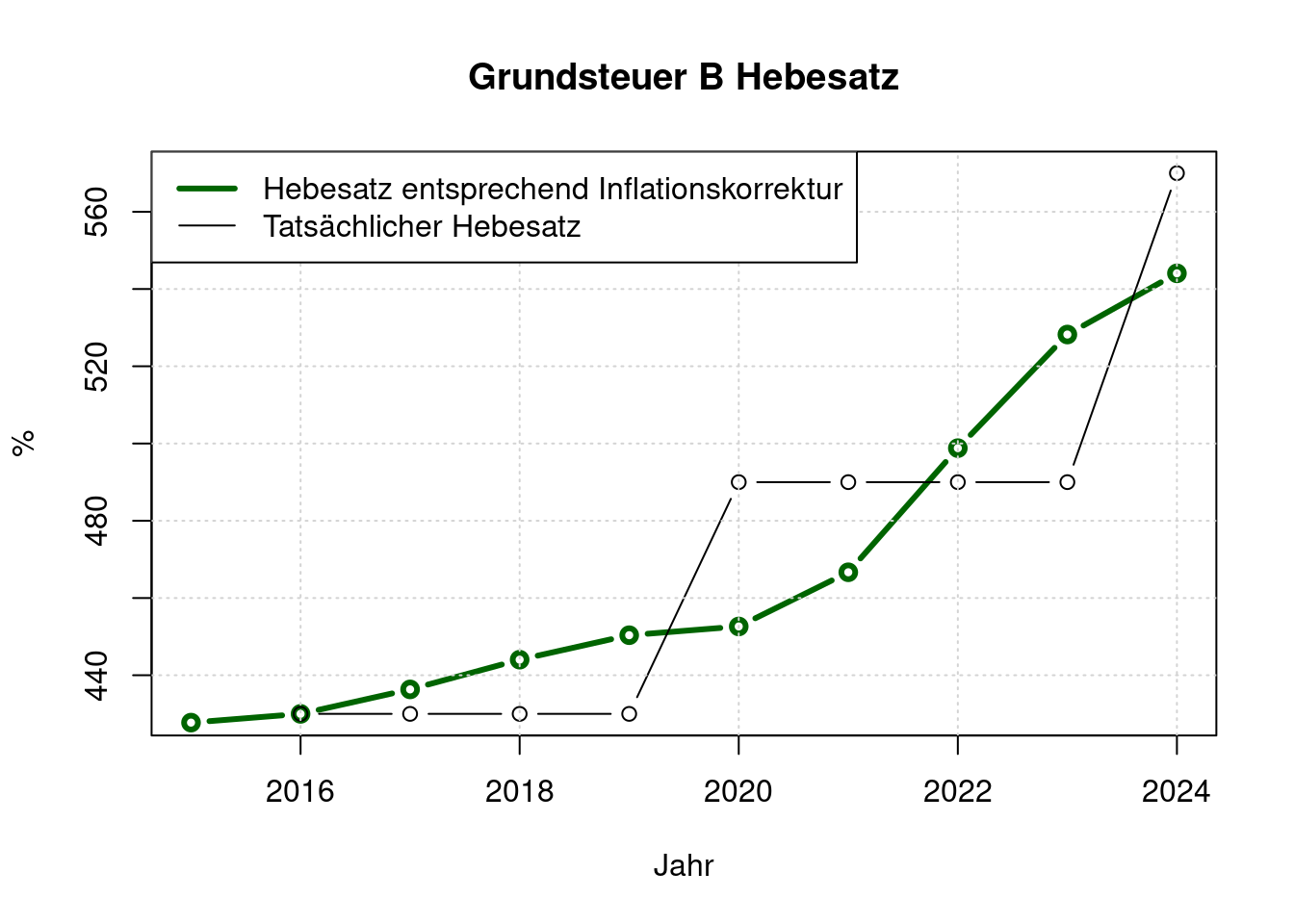
h <- merge(h, inflation);
h$i_grundsteuerb <- h$h_grundsteuerb[1] * h$index / h$index[1];
plot(h$jahr, h$i_grundsteuerb, type='b',
main='Grundsteuer B Hebesatz',
xlab='Jahr', ylab='%',
col='darkgreen', lwd=3,
ylim=c(0,570));
lines(h$jahr, h$h_grundsteuerb, type='b');
grid();
legend(x= "bottomright",
legend=c("Hebesatz entsprechend Inflationskorrektur ab 2004", "Tatsächlicher Hebesatz"),
col=c("darkgreen", "black"),
lwd=c(3, 1));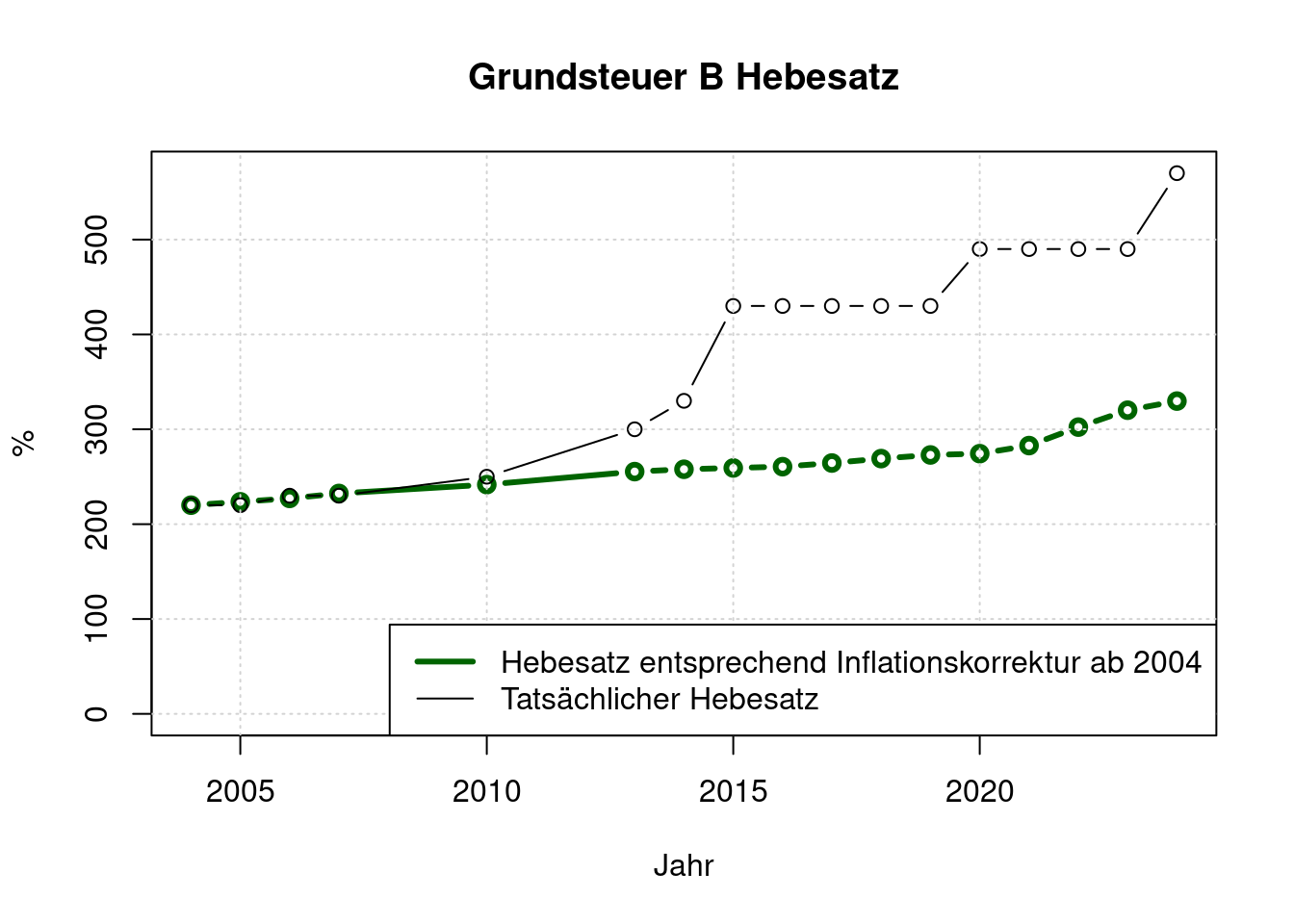
6.1.3 Flächenzunahme?
Die Grundsteuer-Einnahmen haben stärker zugenommen als die Hebesatz B-Erhöhungen. Grundsteuer A ist so wenig, dass man man die resultierende Ungenauigkeit wohl ignorieren kann.
grundsteuer_roh <- e$grundsteuer * e$index / max(e$index)
(grundsteuer_roh[10] / e$h_grundsteuerb[10]) / (grundsteuer_roh[2] / e$h_grundsteuerb[2])## [1] 1.163532Das deutet ganz grob darauf hin, dass die bebaute Fläche von Bürstadt seither um 16% zugenommen hat. Allerdings gehen in die Berechnung des Einheitswerts durch das Finanzamt weitere Parameter ein.
7 Demografische Entwicklung
7.1 Entwicklung der Einwohnerzahl
Einwohnerzahl 2012 bis 2022: https://www.wegweiser-kommune.de/daten/demografische-entwicklung+buerstadt+2012-2022+tabelle
Einwohnerzahl 2023: https://www.buerstadt.de/de/rathaus-politik/ueber-buerstadt/meldungen-und-termine?c7-item=6046599
Zwischen den Daten der beiden Quellen für 2022 gibt es eine Abweichung von 291 Bürger*innen, daher zählen wir zu jedem Wert 291 hinzu, damit es 2023 keinen Sprung gibt. Die Werte für 2024 und 2025 sind extrapolationen.
# 2012 2013 ... 2022
ncitizen <- c(15551, 15625, 15802, 16060, 16176, 16315, 16398, 16453, 16492, 16430, 16734);
ncitizen <- ncitizen + 291;
ncitizen[12] <- 17378;
peryear <- coef(lm(ncitizen~jahr, data.frame(jahr=2012:2023, ncitizen)))[2];
ncitizen[13] <- ncitizen[12] + peryear;
ncitizen[14] <- ncitizen[13] + peryear;
plot(2012:2025, ncitizen,
type='b',
xlab='Jahr',
main='Bevölkerungsentwicklung Bürstadt');
grid();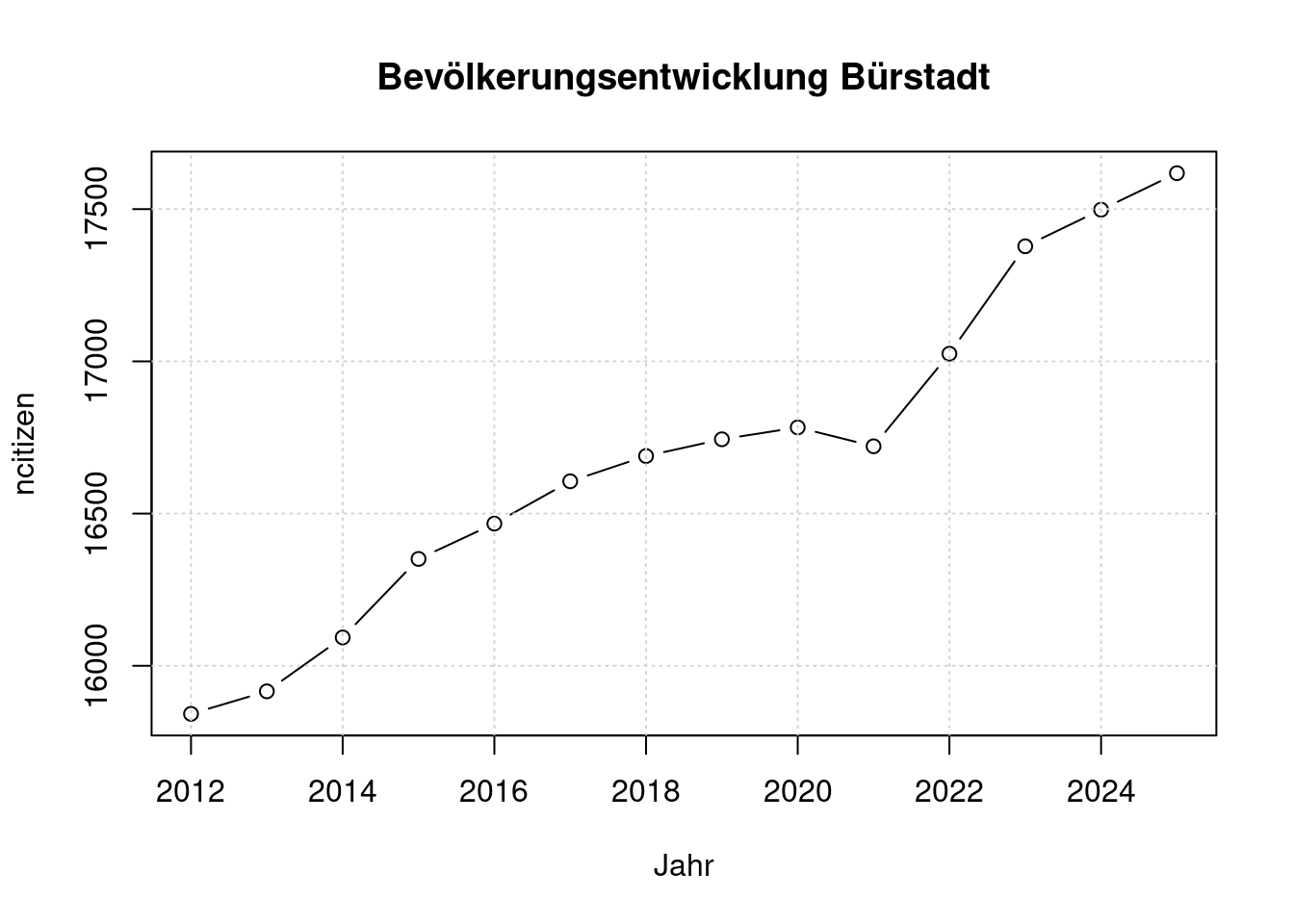
7.2 Verschuldung pro Einwohner*in
n <- subset(a, jahr>=2012);
n$ncitizen <- ncitizen;
plot(n$jahr, n$bereinigt/n$ncitizen,
type='b',
ylab='€',
main='Verschuldung inflationsbereinigt pro Bürger*in');
grid();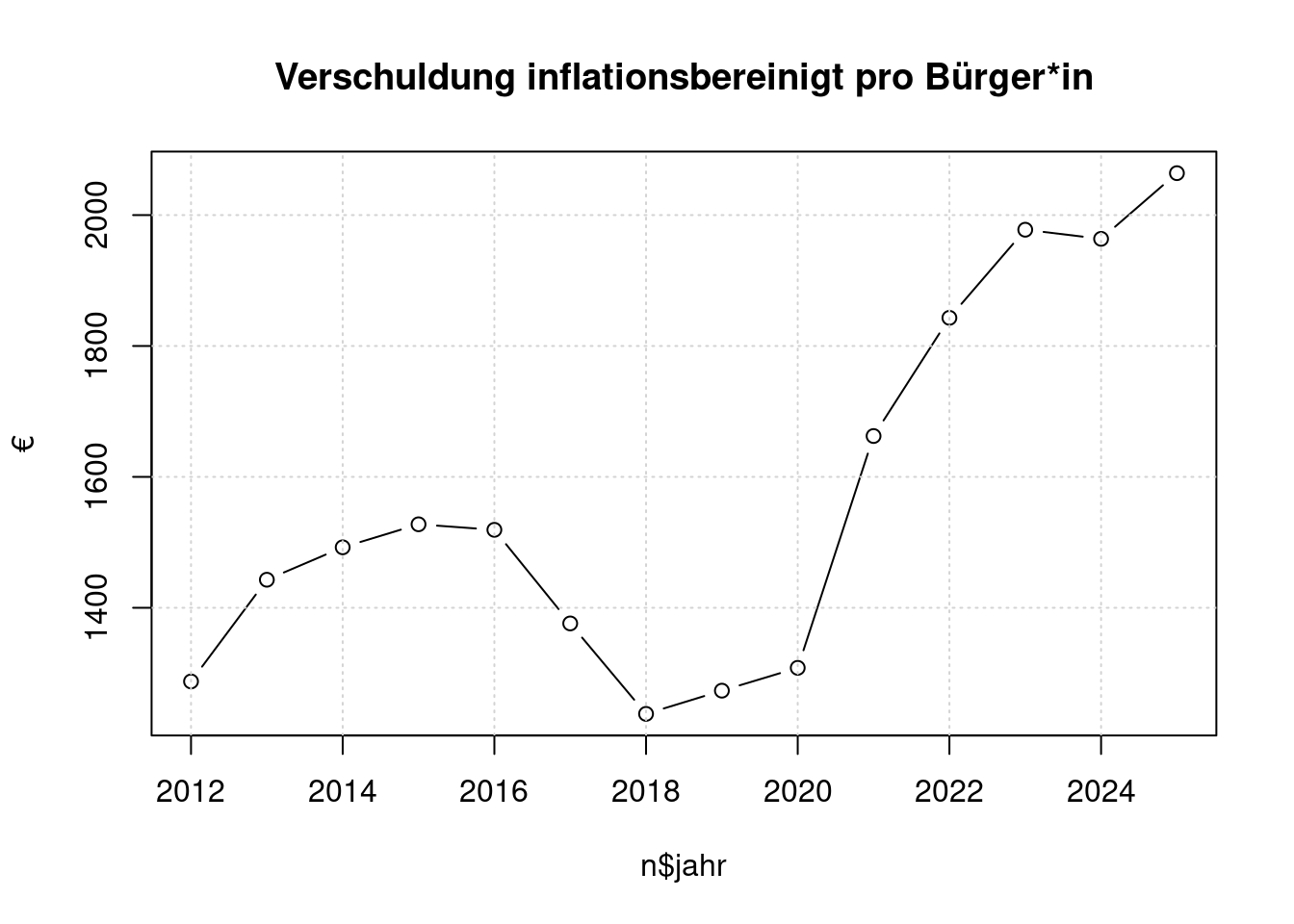
Zunahme gesamt:
ncitizen[length(ncitizen)]/ncitizen[1];## [1] 1.112119Zunahme etwa 11% in 14 Jahren ist deutlich niedriger als 16 % mehr Grundsteuer in 10 Jahren. Vermutlich hat der Flächenbedarf je Bürger*in zugenommen.
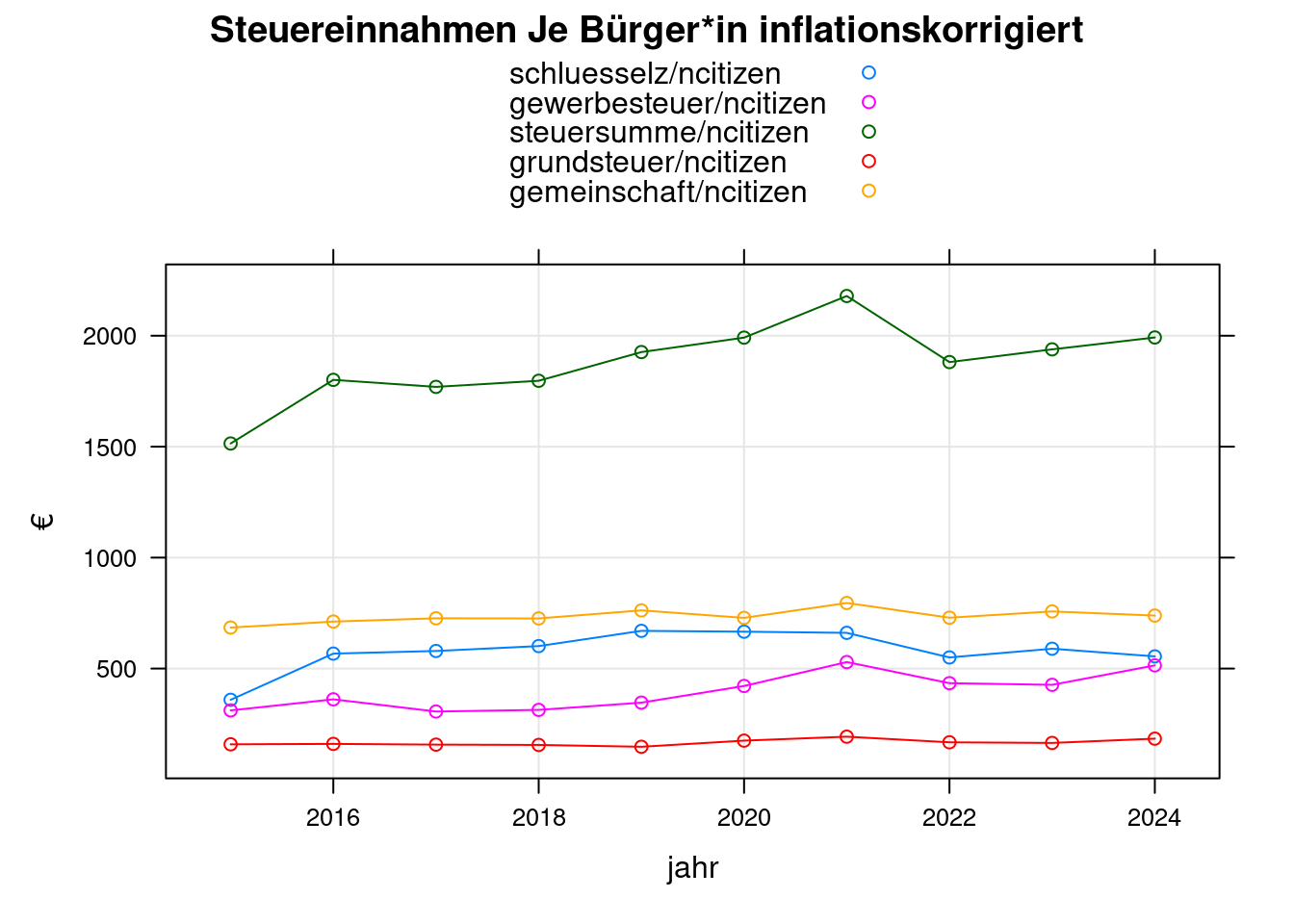
7.3 Steuereinnahmen je Einwohner*in
e$ncitizen <- subset(n, jahr>=2015 & jahr<=2024)$ncitizen
xyplot(schluesselz/ncitizen+gewerbesteuer/ncitizen+steuersumme/ncitizen+grundsteuer/ncitizen+gemeinschaft/ncitizen~jahr,
e, type=c('b','g'), auto.key=TRUE,
main="Steuereinnahmen Je Bürger*in inflationskorrigiert",
ylab="€");