1 Abstract
2 Gerader Anstieg
- 2.1 Eingangssignal
- 2.2 Modellierung des mittleren Bereichs
3 Realer CO2-Anstieg
- 3.1 Wir laden die Realen CO2-Werte:
- 3.2 Ungenauigkeiten
4 Fazit

1 Abstract

Bei der Analyse der Globalen Temperatraturentwicklung 2023 habe ich eine Abschätzung der Klimasensitivität anhand des Verhältnisses aus dem Anstieg aus den CO₂-Emissionen und dem Anstieg der weltweiten Temperatur vorgenommen. Diese Vorgehensweise ist fragwürdig und ungenau. Für den Sonderfall eines konstanten Anstieg von log₂(co2/280) funktioniert die Berechnung dennoch, wie hier gezeigt wird.

Da der reale CO₂ - Gehalt der Athmosphäre nicht exakt linear ansteigt, ergibt sich eine Ungenauigkeit, die wir etwas genauer betrachten.

2 Gerader Anstieg

2.1 Eingangssignal

Als Eingangssignal erzeigen wir uns ein Signal für ein einen konstanten Anstieg der Anregung:

N <- 1000;
START <- 100;
END <- 200;
MIDDLE <- N-START-END;
ECS <- 3.0;
inp <- rep(0, N);
inp[(START):(N-END)] <- 0:MIDDLE /MIDDLE;
inp[(N-END):N] <- 1.0;

t <- 1900 + 0:(N-1) * (2050-1900)/MIDDLE;

plot(t, inp, type='l', main='Eingangssignal', xlab='');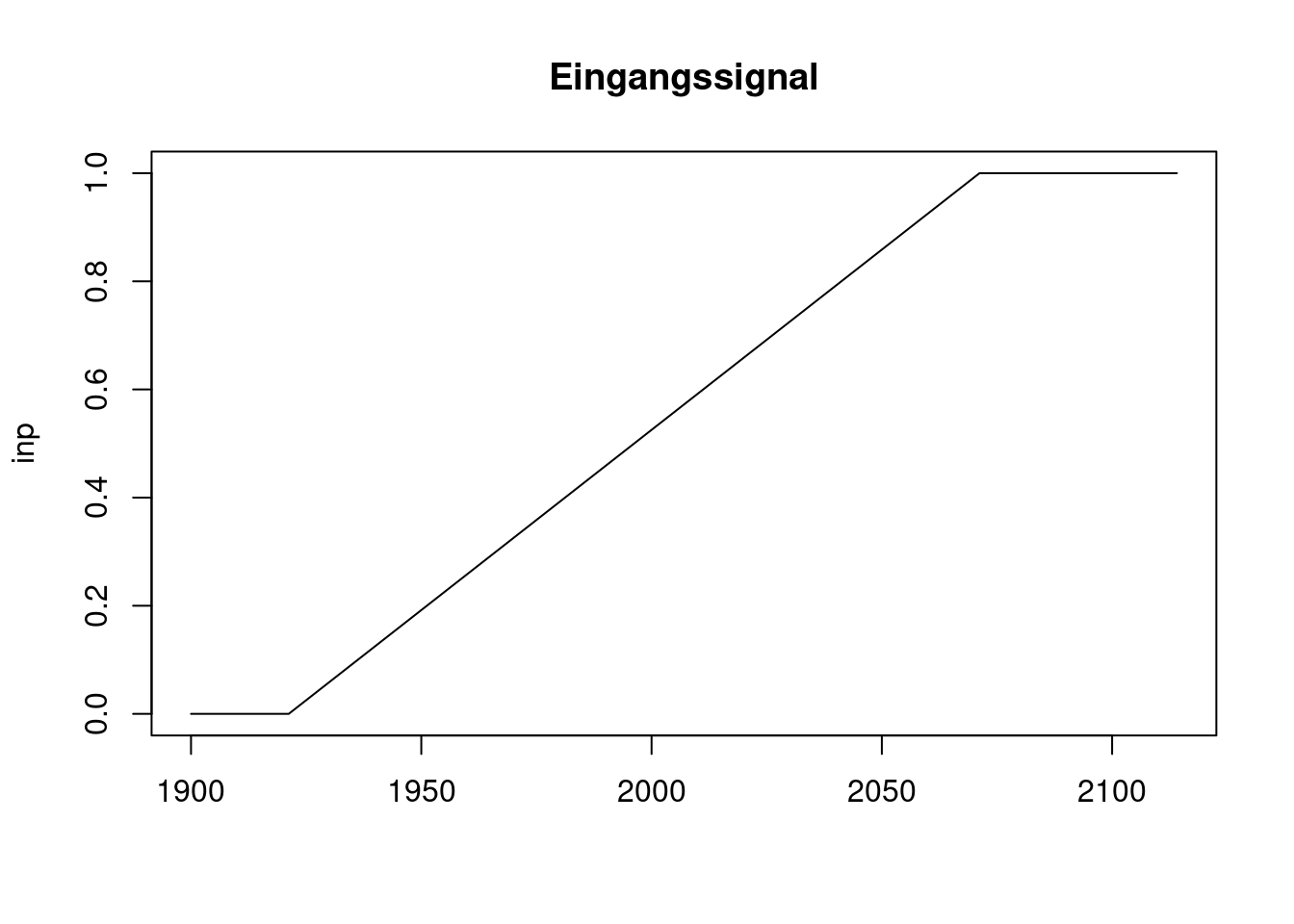

Zur Filterung verwenden wir einen einfachen IIR-Filter (Infinite-Impulse-Response):

lowpass <- function(inp, lambda) {

value <- mean(inp[1:10]);
result <- 0;
i <- 1;
while (i<=length(inp))
{
    value = value*(1-lambda) + inp[i]*lambda;
    result[i] = value;
    i = i+1;
}

result;
}

Nun erzeugen wir simulierte Ausgangssignale für PT1, PT2 und PT3-Systeme und ein ein kombiniertes Signal combined:

LAMBDA <- 16.0;
pt0 <- ECS * inp;
pt1 <- lowpass(pt0 , LAMBDA / MIDDLE);
pt2 <- lowpass(pt1 , LAMBDA / MIDDLE);
pt3 <- lowpass(pt2 , LAMBDA / MIDDLE);
combined <- (pt1 + pt2 + pt3) / 3;

df <- data.frame(t, inp, pt0, pt1, pt2, pt3, combined);
inp <- NULL;
pt0 <- NULL;
pt1 <- NULL;
pt2 <- NULL;
pt3 <- NULL;
combined <- NULL;

library(lattice);
xyplot(pt0+pt1+pt2+pt3+combined~t, data = df, ylab='',
       main='Gegenüberstellung PTx', type=c('g','l'), auto.key=TRUE, xlab='');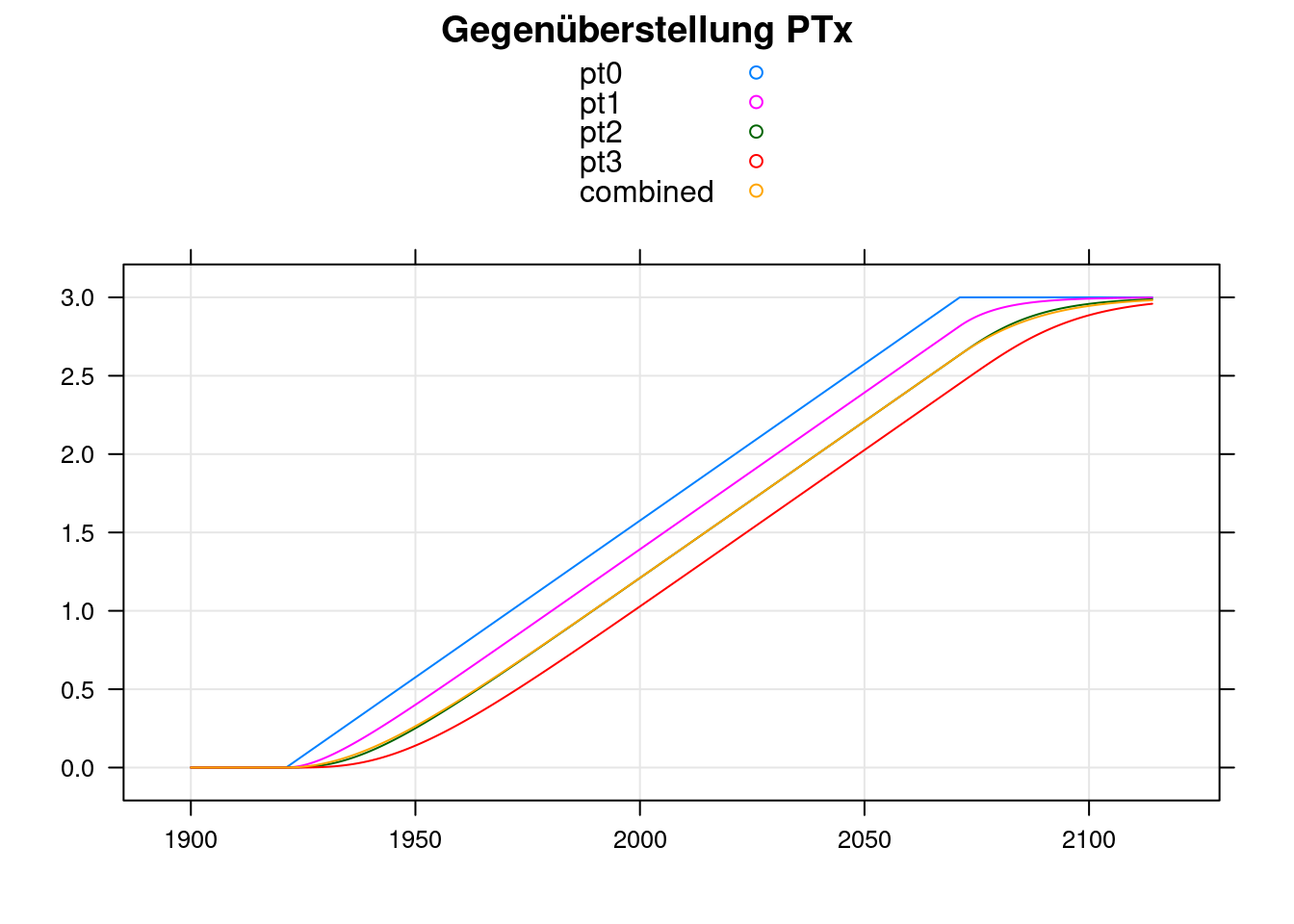

Alle modellierten Systeme weisen unabhängig voneinander für den Zeitraum 1970 bis 2050 dieselbe Steigung und für den Zeitraum nach 2100 denselben Endwert ECS auf.

2.2 Modellierung des mittleren Bereichs

Wenig überraschend weisen alle PTx-Modelle im mittleren Bereich dieselbe Steigung wie das Eingangssignal auf:

t <- NULL;
s <- subset(df, t>=1979 & t<=2024);
xyplot(pt0+pt1+pt2+pt3+combined~t, data = s, ylab='',
       main='Zeitausschnitt', type=c('g','l'), auto.key=TRUE, xlab='');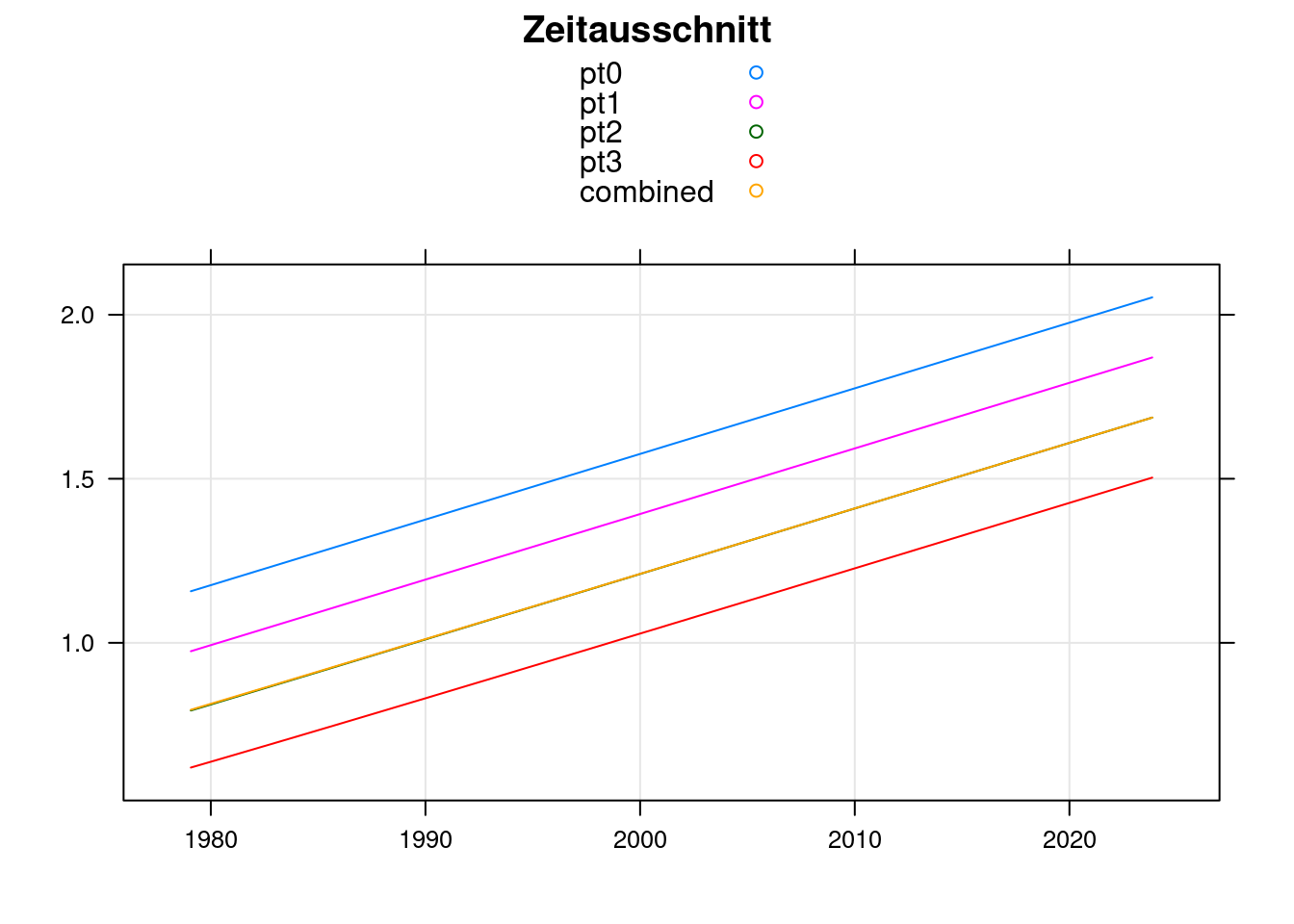

coef(lm(s$pt1 ~ s$t))[2]

##        s$t 
## 0.01999407

coef(lm(s$pt2 ~ s$t))[2]

##        s$t 
## 0.01994925

coef(lm(s$pt3 ~ s$t))[2]

##        s$t 
## 0.01977704

coef(lm(s$combined ~ s$t))[2]

##        s$t 
## 0.01990679

Die Steigung des Eingangssiignals war ein Anstieg von 0.0 auf 1.0 dividiert durch die für den Eingangs-Anstrieg angesetzte Zeit in Jahren:

1.0/(df$t[N-END]-df$t[START])

## [1] 0.006666667

Ein schätzert für ECS berechnet sich also aus dem Unterschied der Steigungen:

dinp <- coef(lm(s$inp ~ s$t))[2]
coef(lm(s$pt1 ~ s$t))[2] / dinp

##      s$t 
## 2.999111

coef(lm(s$pt2 ~ s$t))[2] / dinp

##      s$t 
## 2.992388

coef(lm(s$pt3 ~ s$t))[2] / dinp

##      s$t 
## 2.966556

coef(lm(s$combined ~ s$t))[2]  / dinp

##      s$t 
## 2.986018

Wie zu erwarten war. Unabhängig davon, ob die Verzögerung ein PTx-System 0, 1., 2. oder N-ter Ordnung, eine Totzeit oder eine Kombination daraus ist, lässt sich die Klimasensitvität ECS aus der Steigerungsrate der Ausgangstemperatur abschätzen.

Voraussetzung dafür ist aber ein Lineares System und die Eingangsgröße muss linear ansteigend sein.

3 Realer CO2-Anstieg

Jedoch ist der Anstieg des CO2-Gehalts der Erdamosphäre keine exakte Gerade. Dadurch stimmen die Berechnungen nicht mehr genau.

3.1 Wir laden die Realen CO2-Werte:

Die Veränderung des CO₂-Gehalts in der Atmosphäre laden wir von ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_weekly_mlo.csv Die Datei enthält wöchentliche Angaben der auf Mauna Loa gemessenen CO₂-Konzentration. Es gibt Lücken in der Aufzeichnung, die wir bei der Umwandlung in eine Zeitreihe auffüllen müssen.

co2_weekly <- read.table(pipe("grep -v '^#' co2_weekly_mlo.csv"), sep=",", header=T);
co2w <- rep(co2_weekly$average[1],(df$t[N]-df$t[1])*52);
i <- 1;
n <- 1;

while (i <= length(co2_weekly$decimal))
{
    if (co2_weekly$decimal[i] > df$t[1])
    {
        x <- as.integer((co2_weekly$decimal[i] - df$t[1]) * 365.25 / 7) + 1;
        if (x>=1 && x<=length(co2w) ) {
           if (co2_weekly$average[i]>0) {
               co2w[x] = co2_weekly$average[i];
           }
           co2w[x+1] = co2w[x];
        }
    }
    
    i = i+1;
}
co2w[x:length(co2w)] <- co2w[x];

co2t <- df$t[1] + (0:(length(co2w)-1))/length(co2w) * (df$t[N]-df$t[1]) ;

library(interp);
co2 <- approx(co2t, co2w, n=N)$y;

Für die Zeit vor dem Beginn der Mauna Loa Aufzeichnungen benutzen wir die Werte aus dem Eisbohrkern. Law Dome ice core, Antarctica. Reference: Etheridge, D.M., L.P. Steele, R.L. Langenfelds, R.J. Francey, J.-M. Barnola, and V.I. Morgan. 1996. Natural and anthropogenic changes in atmospheric CO2 over the last 1000 years from air in Antarctic ice and firn. Journal of Geophysical Research 101:4115-4128. http://cdiac.ornl.gov/ftp/trends/co2/lawdome.smoothed.yr20

lawdome <- read.table(pipe("grep '^[[:space:]]*19' lawdome.smoothed.yr20"), sep="", header=F);
lawdome$year <- lawdome$V1; lawdome$V1<-NULL;
lawdome$co2 <- lawdome$V2; lawdome$V2<-NULL;

NLAWDOME <- as.integer( (lawdome$year[length(lawdome$year)]-lawdome$year[1]) * N / (df$t[N] -df$t[1]) );
co2[1:NLAWDOME] <- approx(lawdome$year, lawdome$co2, n=NLAWDOME)$y;

Das neue Modell-Eingangssignal sind jetzt die realen CO₂-Messwerte seit 1900:

inp <- co2;
plot(df$t, inp, type='l', main='Eingangssignal', xlab='');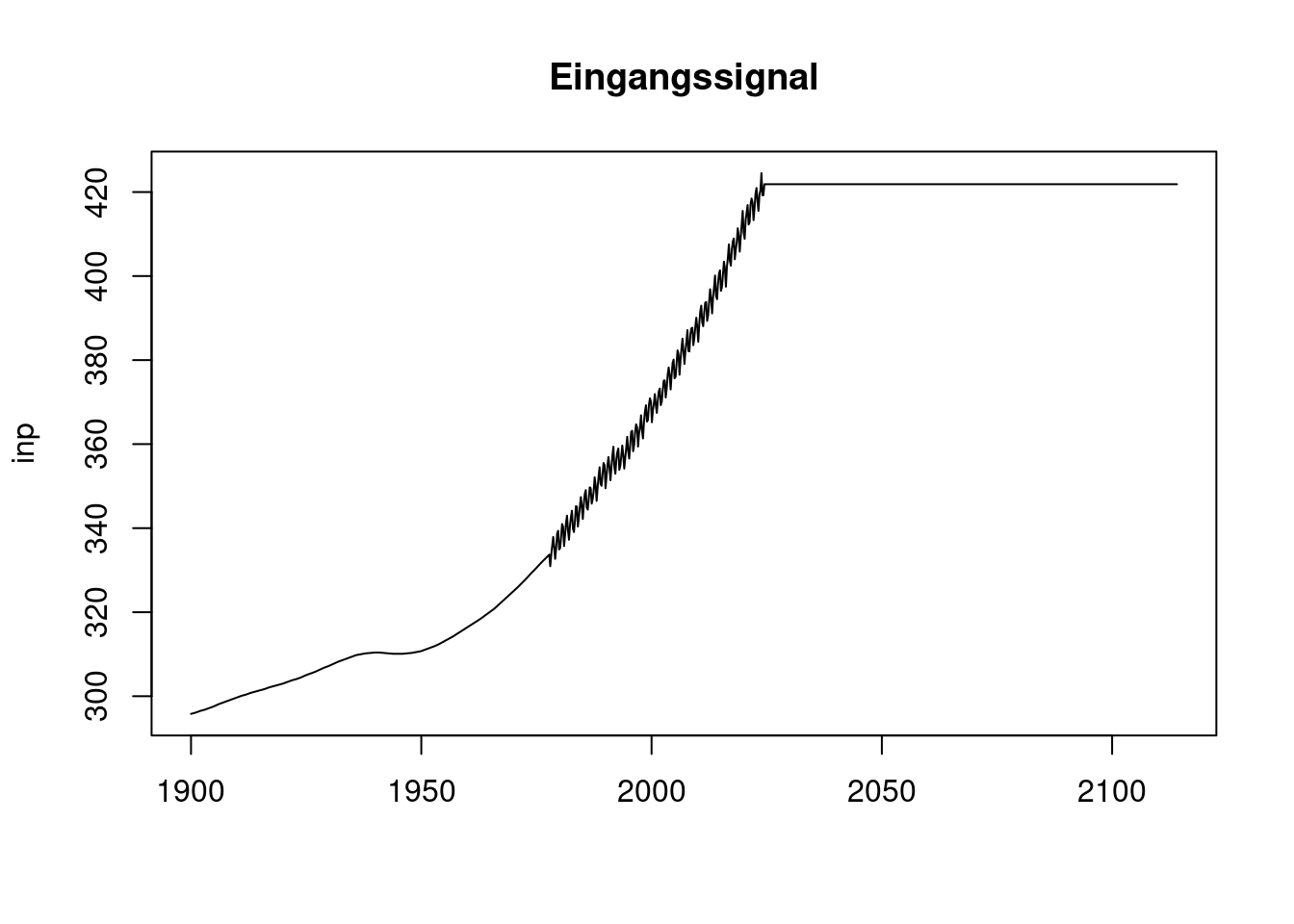

t <- df$t;
pt0 <- ECS * log2(inp / 280);
pt1 <- lowpass(pt0 , LAMBDA / MIDDLE);
pt2 <- lowpass(pt1 , LAMBDA / MIDDLE);
pt3 <- lowpass(pt2 , LAMBDA / MIDDLE);
combined <- (pt1 + pt2 + pt3) / 3;

dfco2 <- data.frame(t, inp, pt0, pt1, pt2, pt3, combined);
t <- NULL;
inp <- NULL;
pt0 <- NULL;
pt1 <- NULL;
pt2 <- NULL;
pt3 <- NULL;
combined <- NULL;

sco2 <- subset(dfco2, t>=1979 & t<=2024);
xyplot(pt0+pt1+pt2+pt3+combined~t, data = sco2, ylab='',
       main='Zeitausschnitt mit CO2-Anregung', type=c('g','l'), auto.key=TRUE, xlab='');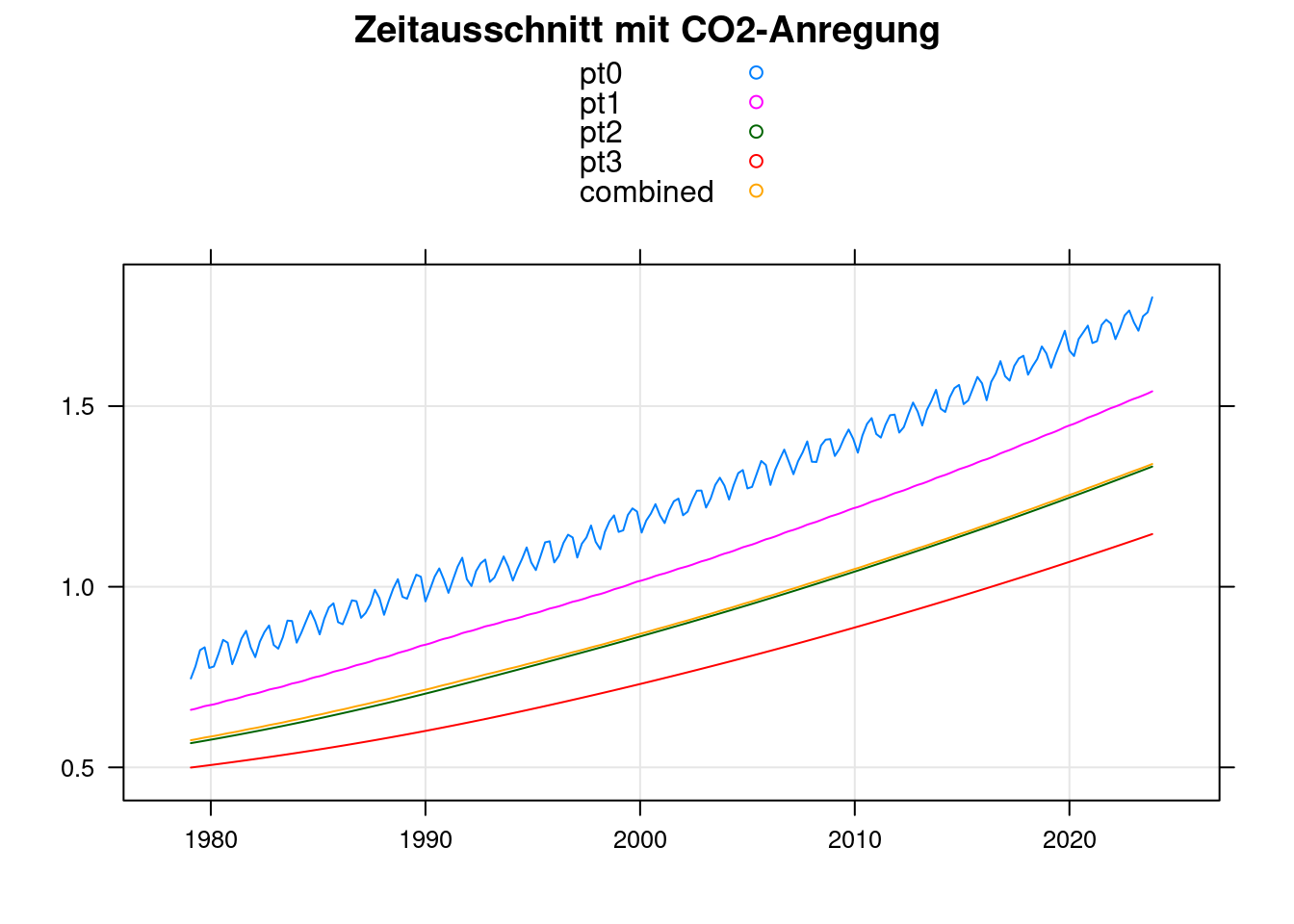

3.2 Ungenauigkeiten

Wir wenden nun dieselbe Methode zur Schätzung der Klimasensitivität ECS nun auf das Pt1, Pt2 und Pt3 System an. Die Korrekte ECS haben wir oben als 3,0 °C / Verdoppelung eingesetzt. Die Schätzwerte sind:

estimate_ecs <- function(ptx) {
#    fit <- nls(ptx ~ A + B*log(inp/280), data = sco2,
#               start = list( A=0, B=0.01) );
#
#    steigung <- coef(fit)[2];
#    log(2) * steigung;
     as.double( log(2) * coef( lm(ptx ~ log(sco2$inp/280) ) )[2] );
}

estimate_ecs( sco2$pt0 );

## [1] 3

estimate_ecs( sco2$pt1 );

## [1] 2.690568

estimate_ecs( sco2$pt2 );

## [1] 2.366939

estimate_ecs( sco2$pt3 );

## [1] 2.010192

estimate_ecs( sco2$combined );

## [1] 2.3559

4 Fazit

Die Größe der Ungenauigkeit hängt von der Ordnung des Systems und von den Zeitkonstanten ab.

Für die Erwärmung der Weltmeere sind sehr lange Zeitkonstanten zu erwarten.

Auffällig ist, dass die auf diese Weise geschätzte Sensitivität immer zu klein zu sein scheint. Für nichtlineare Systemanteile ist aufgrund von vermuteten Kippunkten des Klimasystems eher eine größe Klimasensitivität zu erwarten.

Wenn also für die realen Temperaturmesswerte des Weltklimas mit diesem einfachen Verfahren eine Klimasensitivität von 3,0°C für eine Verdoppelung des CO₂ geschätzt wird und diese Methode dazu neigt, die Klimasensitivität zu unterschätzen, dann ist eher zu vermuten, dass die Klimasensitivität wahrscheinlich höher ist als der “Best Guess” des IPCC.

Verhalten von PTx-Systemen bei stetig steigendem Eingangssignel

Bernd Herd

10. Jan 2024