1 Abstract

Im Januar 2024 habe habe ich diese R-Skripte zur Analyse der Temperatur-Zeitreihen entwickelt. Diese Version wendet dieselben Skripte auf die Temperatur-Messreihen bis Oktober 2024 an.

Die Texte sind nicht aktualisiert. Die Neuen Messdaten vom Oktober 2024 sind erschreckend.

Um die auffälligen Temperaturmessungen von 2023 zu bewerten, untersuchen wir die von climatereanalyzer.org bereitgestellten Temperaturmeßwerte und vergleichen sie mit CO2, ENSO und Sonnenflecken-Meßwerten um die Entwicklung von 2023 zu bewerten.

Die Meßwerte sind tatsächlich auffällig, aber nicht so extrem wie es in vielen Diskussionen behauptet wird.

2 Einleitung

Die weltweite mittlere Temperatur ist 2023 quasi sprunghaft gestiegen. In wissenschaftlich interessierten Kreisen wurde dies seit Juni 2023 diskutiert. Der Öffentlichkeit wurde dies im Zusammenhang mit den Überflutungen im Winter 2023 auch im Fernsehen erläutert.

Insbesondere die Darstellung von https://climatereanalyzer.org/clim/t2_daily/?dm_id=world wurde diese Jahr in Social Media gepostet.

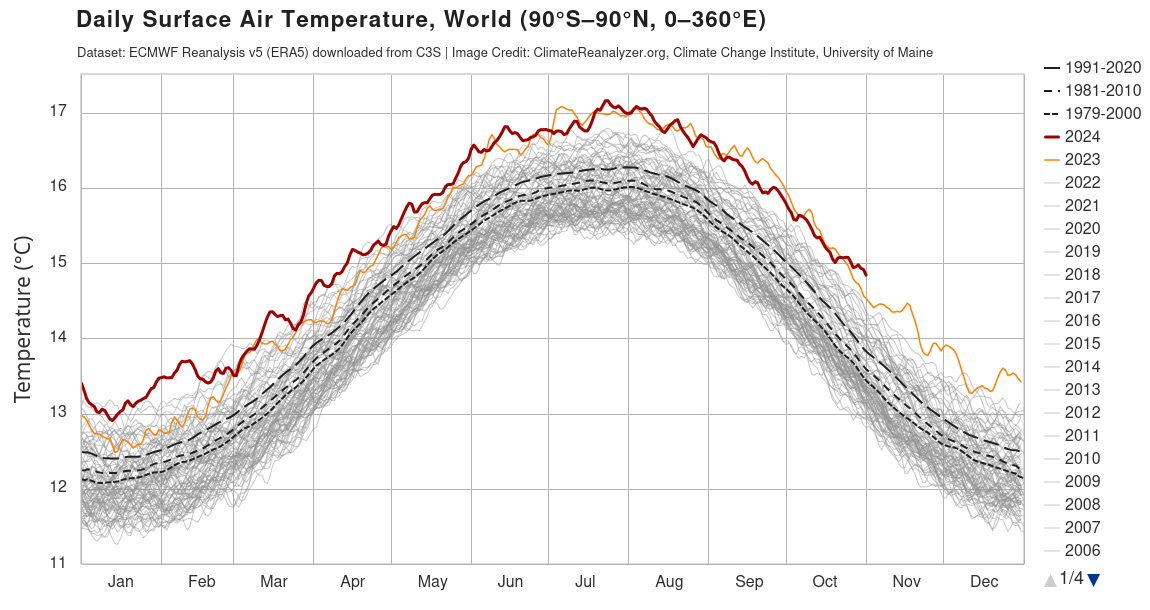
In diesem Dokument geht es um eine Einordnung der Entwicklung der Temperatur im Vergleich zu früheren Jahrzehnten durch eine mathematische Analyse.

3 Wissenschaftliche Rezeption

3.1 Hansen et al.

Eine Forschergruppe rund um den berühmten Klimawissenschaftler James Hansen hat 2023 eine neue Wissenschaftliche Arbeit herausgebracht, die nahelegt, dass der IPCC die Klimasensitivität der Erde bislang grob unterschätzt hat. Die besten Schätzungen des IPCC liegen bei etwa 3°C. Hansen schätzt die Klimasensitivität der Erde stattdessen in seiner neuesten Arbeit auf ca. 4,8°C. Die Auswirkungen einer so hohen Klimasensitivität für die Menschheit wären verheerend.

https://academic.oup.com/oocc/article/3/1/kgad008/7335889?searchresult=1

3.2 Michael E. Mann

Diese Arbeit hat in der Presse erhebliche Aufmerksamkeit erhalten. Dabei gibt es auch erheblichen Widerspruch zur Arbeit von Hansen, unter Anderem von dem ebenfalls berühmten Klimawissenschaftler Michael E. Mann. Dieser verweist auf Mastodon auf jeden Presseartikel, in dem er der Auffassung von Hansen widerspricht.

Zum Beispiel:

    Mann responded to Hansen’s paper within a few days of its publication in November.
    After a few ritual expressions of respect for Hansen’s record, he got down to business:
    “I feel that this latest contribution from Jim and his co-authors is at best
    unconvincing,” said Mann. (What would “at worst” be, then?)

    “I don’t think they have made the case for their main claims, i.e. that warming is
    accelerating, that the planetary heat imbalance is increasing, that aerosols are playing
    some outsized role, or that climate models are getting all of this wrong.

3.3 Gavin Schmidt

Der bekannte US-Amerikanische Klimawissenschaftler Gavin Schmidt, Leiter des GISS-Instituts der NASA hat Anfang 2024 einen Artikel im Realclimate Blog veröffentlicht.

https://www.realclimate.org/index.php/archives/2024/01/annual-gmsat-predictions-and-enso/ Woriin er:

  • Bestätigt, dass die Temperatur 2023 höher war als seine Vorhersage für 2023 anhand der ENSO-Vorhersage.
  • Eine Voraussage für die mittlere Jahres-Temperatur für 2024 von 1,38 ± 0,14°C über dem Mittelwert von 1880-1899 macht. Das ist 0,01 °C wärmer als 2023.
  • Die Frage diskutiert, warum die Voraussage für 2023 so weit daneben lag.
  • Auf die von Hansen at al. diskutierte Frage eingeht, ob die Reduktion von SO2 Emissionen aus der Hochseeschiffahrt doch einen höheren Einfluß auf die mittlere Temperatur haben könnte:
    We will also be seeing more comprehensive estimates of the impact of the Hunga-Tonga
    eruption, and also of the impacts of the decreases in marine shipping emissions. 
    It might be that the initial estimates of their impacts were underestimated.

3.4 Tamino Blog

Ein Mathematiker hat in seinem Blog einen interessanten Beitrag zu dem Thema geschrieben, der andere Methoden verwendet und die Details nicht so ausführlich dokumentiert, aber zu ähnlichen Ergebnissen kommt:

https://tamino.wordpress.com/2024/01/05/global-warming-picks-up-speed/

Die Arbeit von Hansen stellt eine mögliche Erklärung für die sehr hohen Temperatur-Messwerte 2023 dar. In dieser Analyse versuche ich, eine fundierte Meinung zu finden, ob ich mich eher der Auffassung von James Hansen, oder eher der Auffassung von Michael E. Mann anschließe.

4 Werkzeuge

Dieses Dokument basiert auf der Software GNU R https://www.r-project.org/, das unter Debian GNU/Linux ausgeführt wird. Der Quellcode ist erhältlich von https://www.herdsoft.com/ftp/reanalyzer-2024-11-06.zip

5 Analyse der Zeitreihe

Als Ausgangsbasis laden wir die Rohaden von https://www.climatereanalyzer.org/clim/t2_daily/json/era5_world_t2_day.json herunter. Sie liegen im JSON-Format vor.

library(jsonlite)
d <- fromJSON("era5_world_t2_day.json")

Die Daten liegen nun in R als data.frame vor. unter d$name sind den Zeilen die Jahresnamen zugeordnet. Jeder Eintrag umfasst also die Daten eines Jahres. Die letzten drei Einträge sind statistische Auswertungen.

d$name;
##  [1] "1940"      "1941"      "1942"      "1943"      "1944"      "1945"     
##  [7] "1946"      "1947"      "1948"      "1949"      "1950"      "1951"     
## [13] "1952"      "1953"      "1954"      "1955"      "1956"      "1957"     
## [19] "1958"      "1959"      "1960"      "1961"      "1962"      "1963"     
## [25] "1964"      "1965"      "1966"      "1967"      "1968"      "1969"     
## [31] "1970"      "1971"      "1972"      "1973"      "1974"      "1975"     
## [37] "1976"      "1977"      "1978"      "1979"      "1980"      "1981"     
## [43] "1982"      "1983"      "1984"      "1985"      "1986"      "1987"     
## [49] "1988"      "1989"      "1990"      "1991"      "1992"      "1993"     
## [55] "1994"      "1995"      "1996"      "1997"      "1998"      "1999"     
## [61] "2000"      "2001"      "2002"      "2003"      "2004"      "2005"     
## [67] "2006"      "2007"      "2008"      "2009"      "2010"      "2011"     
## [73] "2012"      "2013"      "2014"      "2015"      "2016"      "2017"     
## [79] "2018"      "2019"      "2020"      "2021"      "2022"      "2023"     
## [85] "2024"      "1979-2000" "1981-2010" "1991-2020"

Die Zeitreihe beginnt ab 1940. Zunächst mal generieren wir aus den Rohdaten einen Plot, der optisch am die Visualisierung in Climaterealanalyzer angelehnt ist.

plot(x=NULL, y=NULL, type='l', main='Oberflächentemperatur Weltweit', lwd=3,
     xlim=c(0, 365), ylim=c(11, 18), ylab='Temperatur °C', xlab='')
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
i=1;
while (i<length(d$name)-4) {
  lines(d$data[[i]], type='l', col='lightgray')
  i=i+1;
}
lines(d$data[[length(d$name)-4]], type='l', lwd=3, col='orange')
lines(d$data[[length(d$name)-2]], type='l', lty=5)
lines(d$data[[length(d$name)-1]], type='l', lty=2)
lines(d$data[[length(d$name)]], type='l', lty=2)
lines(d$data[[length(d$name)-3]], type='l', lwd=3)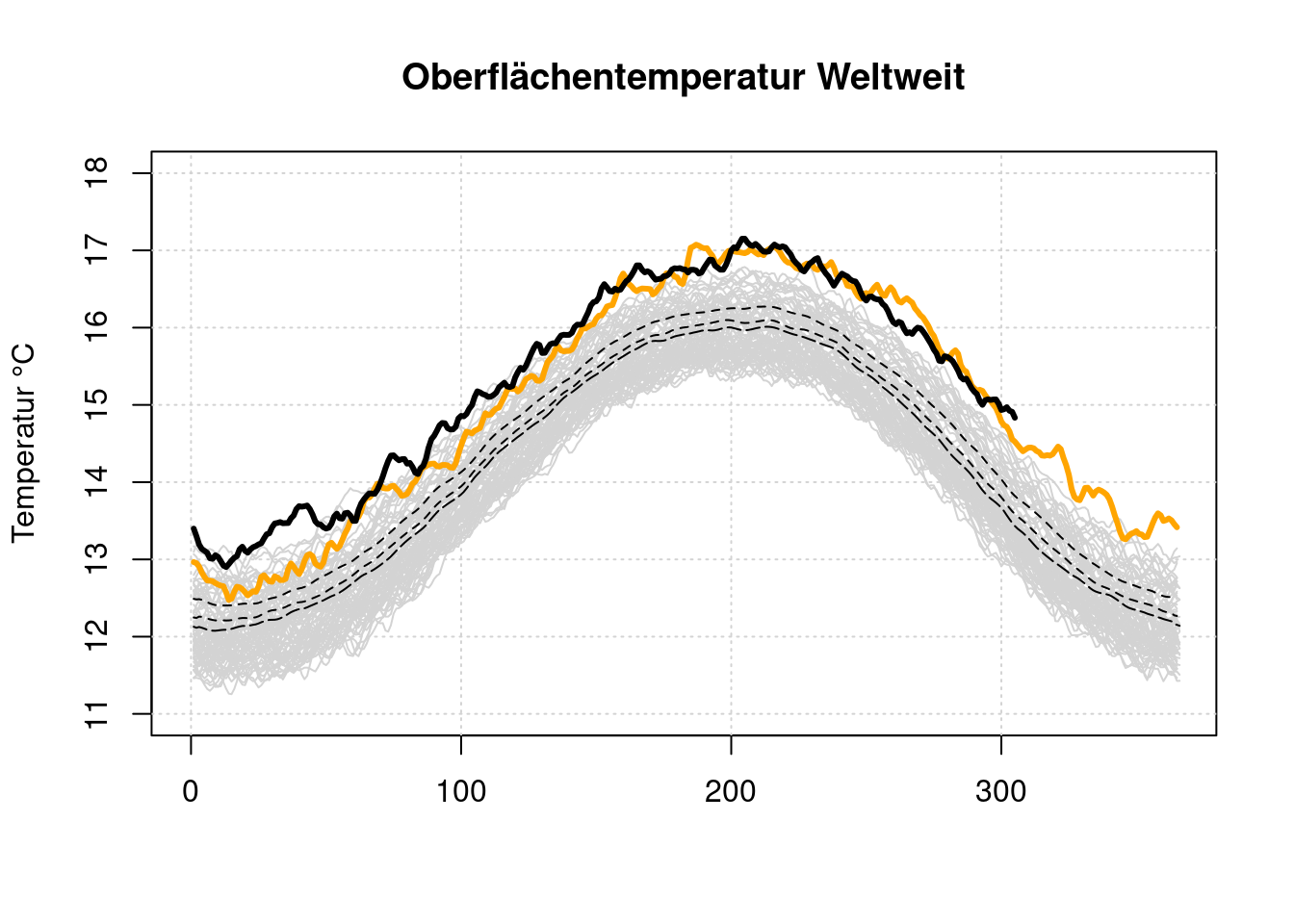

Diese Darstellung betont sehr stark, wie weit die 2023er Kurve oberhalb aller anderen Kurven liegt. Es ist aber nicht erkennbar, ob ein solch schneller Anstrieg der Temperatur auf einem niedrigeren Temperaturniveau in der Vergangenheit auch schon geschehen ist.

Zunächst wandeln wir die nach Jahren organisierten Temperaturen in eine zusammenhängende Zeitreihe ‘timeseries’ um.

Wir bestimmen die Anzahl wirklicher Jahre in Variable years so, dass die Statistikdaten nicht als Jahresdaten falsch interpretiert werden.

years = length(d$name)
while (years > 0 &&
       nchar(d$name[years])>4)
{
  years=years-1;
}

years;
## [1] 85

Für die erste Analyse beginnen wir im Jahr 1940.

timeseries <- 0;
n <- 1;
year <- 1;
while (year <= years)
{
  year_data <- d$data[[year]];
  year_data <- year_data[ !is.na(year_data) ];

  len <- length(year_data);
  timeseries[ n:(n+len-1) ] = year_data;
  n = n + len;
  year = year + 1;
}

t <- as.numeric(d$name[[1]]) + 0:(n-2) * (1/365.25);

plot(t, timeseries, type='l', main='Oberflächentemperatur Weltweit',
     xlab='', ylab='Temperatur °C')
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))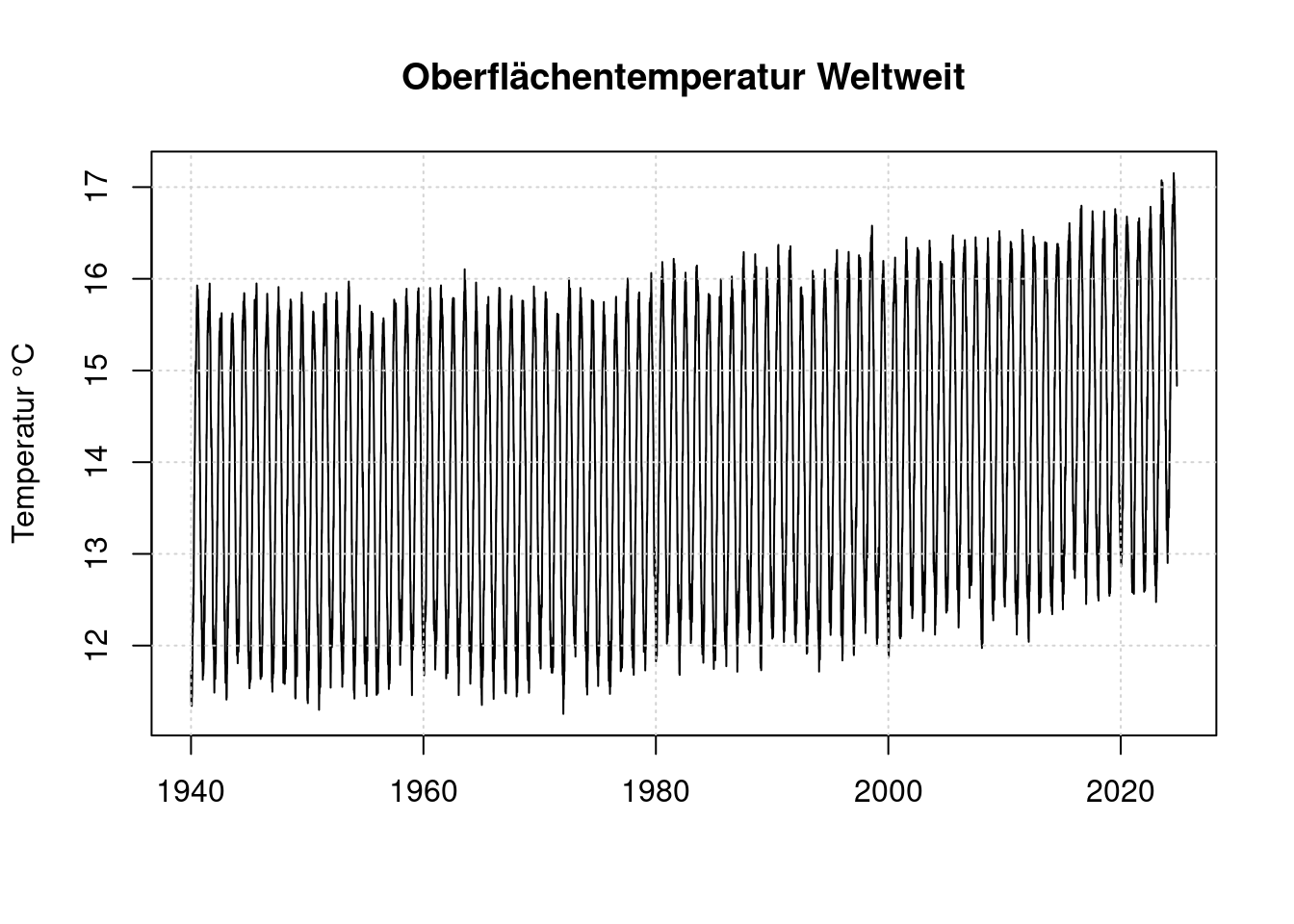

Hier sieht das Extrem von 2023 bei Weitem nicht mehr so beeindruckend aus wie in der Darstellung von clamaterealanyzer.org. Aber der starke Jahresgang versteckt die eigentlichen Unterschiede. Daher bilden wir eine neue Zeitreihe unter Kompensation des Jahresgangs.

6 Berechnung des Jahresgangs

Wir berechnen den Jahresgang als Mittelwert zwischen 1979 und 2022.

season_sum <- rep(0, 365);
year <- 1;
n <- 0;
while (year <= years) {
   if (as.numeric(d$name[year]) >= 1979 &&
       as.numeric(d$name[year]) <= 2022) {
       season_sum = season_sum + d$data[[year]][1:365];
       n <- n + 1;
   }
   year <- year + 1;
}

season_sum[366] <- season_sum[365];
seasonal_avg <- season_sum / n;
# Calculate linear time series as anomaly compared to regular seasonal values
anomaly <- 0;
n <- 1;
year = 1;
while (year <= years)
{
  year_data <- d$data[[year]];

  year_data = year_data-seasonal_avg;
  year_data <- year_data[ !is.na(year_data) ];

  len <- length(year_data);
  anomaly[ n:(n+len-1) ] = year_data;
  n = n + len;
  year = year + 1;
}

plot(t, anomaly, type='l',
     main='Oberflächentemperatur mit Kompensation des Jahresgangs',
     ylab='Temperatur °C', xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))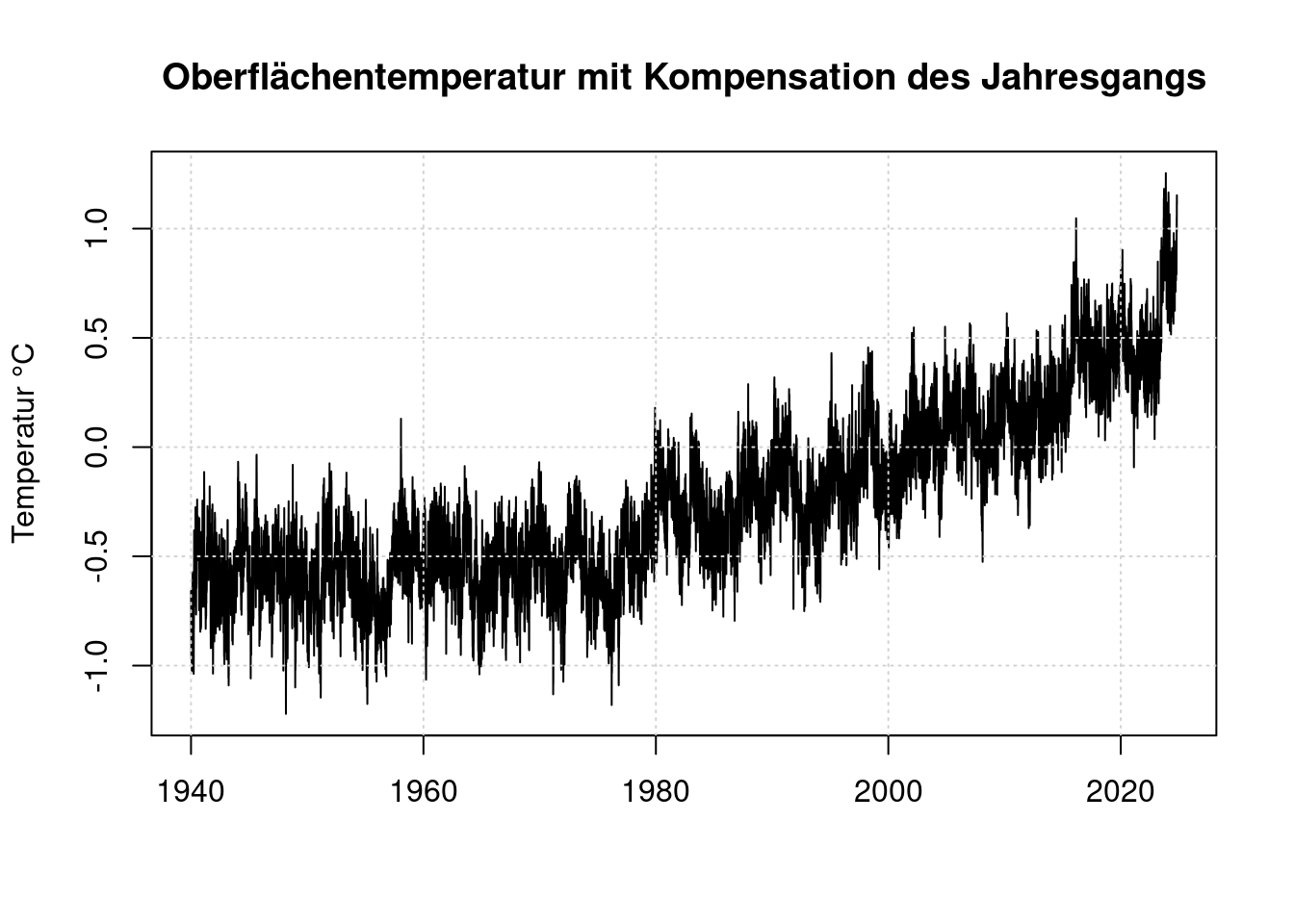

Diese Werte sind relativ zum Mittelwert von 1981-2010. Das sind nicht die vorindustriellen Werte, wie sie die Basis des Pariser Klimaabkommens sind. Vergleiche Stefan Rahmstorf https://scilogs.spektrum.de/klimalounge/2-grad-relativ-zu-wann/

Um den Unterschied zwischen den Mittelwerten 1981-2010 und den Mittelwerten zum Beginn der Industrialisierung zu bestimmen brauchen wir eine Zeitreihe, die ältere Werte enthält.

Als Basiswert für unsere Temperaturen benutzen wir den Zeitraum von 1880 bis 1899, weil Gavin Schmidt diesen in seinem Blogpost verwendet hat.

Wir laden die Gistemp-Daten der NASA als Datei von https://data.giss.nasa.gov/gistemp/tabledata_v4/GLB.Ts+dSST.txt und berechnen die Erwärmung für den Zeitraum 1880 bis 1899 und 1979 bis 2022:

giss <- read.table(pipe("egrep '^18|^19|^20' GLB.Ts+dSST.txt"), sep="", header=F);
giss$year <- as.numeric(giss$V1); giss$V1 <- NULL; giss$V20 <- NULL;
giss$j_d <- as.numeric(giss$V14)*0.01; giss$V14 <- NULL; giss$V15 <- NULL;
## Warning: NAs durch Umwandlung erzeugt
giss$jan <- as.numeric(giss$V2)*0.01; giss$V2 <- NULL;
giss$feb <- as.numeric(giss$V3)*0.01; giss$V3 <- NULL;
giss$mar <- as.numeric(giss$V4)*0.01; giss$V4 <- NULL;
giss$apr <- as.numeric(giss$V5)*0.01; giss$V5 <- NULL;
giss$may <- as.numeric(giss$V6)*0.01; giss$V6 <- NULL;
giss$jun <- as.numeric(giss$V7)*0.01; giss$V7 <- NULL;
giss$jul <- as.numeric(giss$V8)*0.01; giss$V8 <- NULL;
giss$aug <- as.numeric(giss$V9)*0.01; giss$V9 <- NULL;
giss$sep <- as.numeric(giss$V10)*0.01; giss$V10<- NULL;
giss$oct <- as.numeric(giss$V11)*0.01; giss$V11<- NULL;
## Warning: NAs durch Umwandlung erzeugt
giss$nov <- as.numeric(giss$V12)*0.01; giss$V12<- NULL;
## Warning: NAs durch Umwandlung erzeugt
giss$dec <- as.numeric(giss$V13)*0.01; giss$V13<- NULL;
## Warning: NAs durch Umwandlung erzeugt
mean_1880_1899 <- mean(giss$j_d[(1880-1880+1):(1899-1880+1)]);
mean_1951_1980 <- mean(giss$j_d[(1951-1880+1):(1980-1880+1)]);
mean_1979_2022 <- mean(giss$j_d[(1979-1880+1):(2022-1880+1)]);
difference_1979_1880 <- mean_1979_2022 - mean_1880_1899;
data.frame(mean_1880_1899, mean_1979_2022, difference_1979_1880);
##   mean_1880_1899 mean_1979_2022 difference_1979_1880
## 1        -0.2295      0.5263636            0.7558636
anomaly = anomaly + difference_1979_1880;

plot(t, anomaly, type='l',
     main='Oberflächentemperatur mit Bezugstemperatur 1880 bis 1899',
     ylab='Temperatur °C', xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))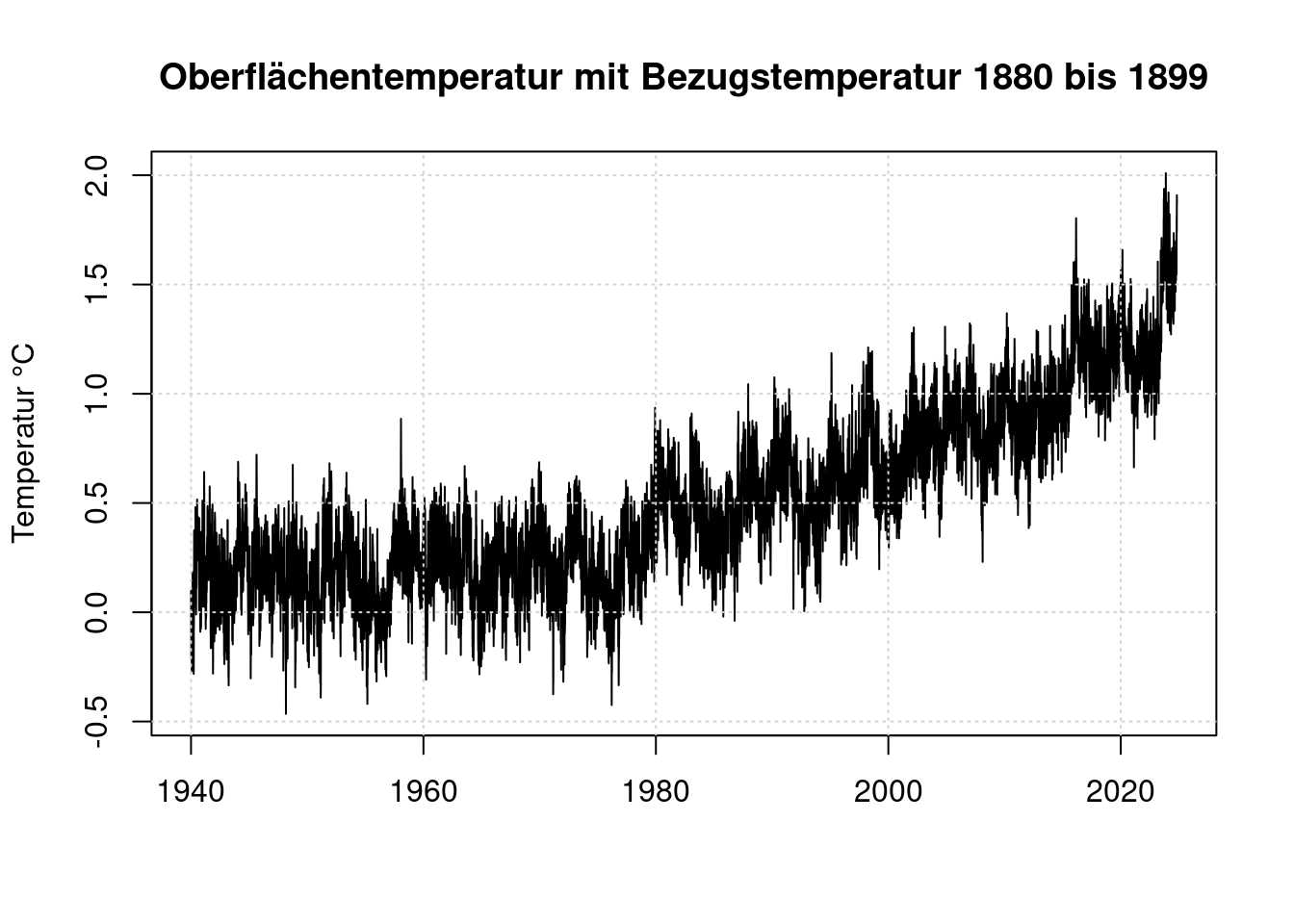

Wie man sieht, begann die weltweite Temperatur ab ca. 1975 gleichmäßig anzusteigen. Für die weitere Betrachtung werten wir nur noch die Daten ab 1979 aus, weil erst für diesen Zeitraum der ENSO-Index verfügbar ist.

startyear = 1;
while (startyear < years &&
       d$name[startyear] != "1979")
{
  startyear=startyear+1;
}
startyear;
## [1] 40
anomaly <- 0;
n <- 1;
year = startyear;
while (year <= years)
{
  year_data <- d$data[[year]];

  year_data = year_data-seasonal_avg;
  year_data <- year_data[ !is.na(year_data) ];

  len <- length(year_data);
  anomaly[ n:(n+len-1) ] = year_data;
  n = n + len;
  year = year + 1;
}

anomaly = anomaly + difference_1979_1880;
t <- as.numeric(d$name[[startyear]]) + 0:(n-2) * (1/365.25)
plot(t, anomaly, type='l',
     main='Oberflächentemperatur mit Kompensation des Jahresgangs',
     ylab='Temperatur °C', xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))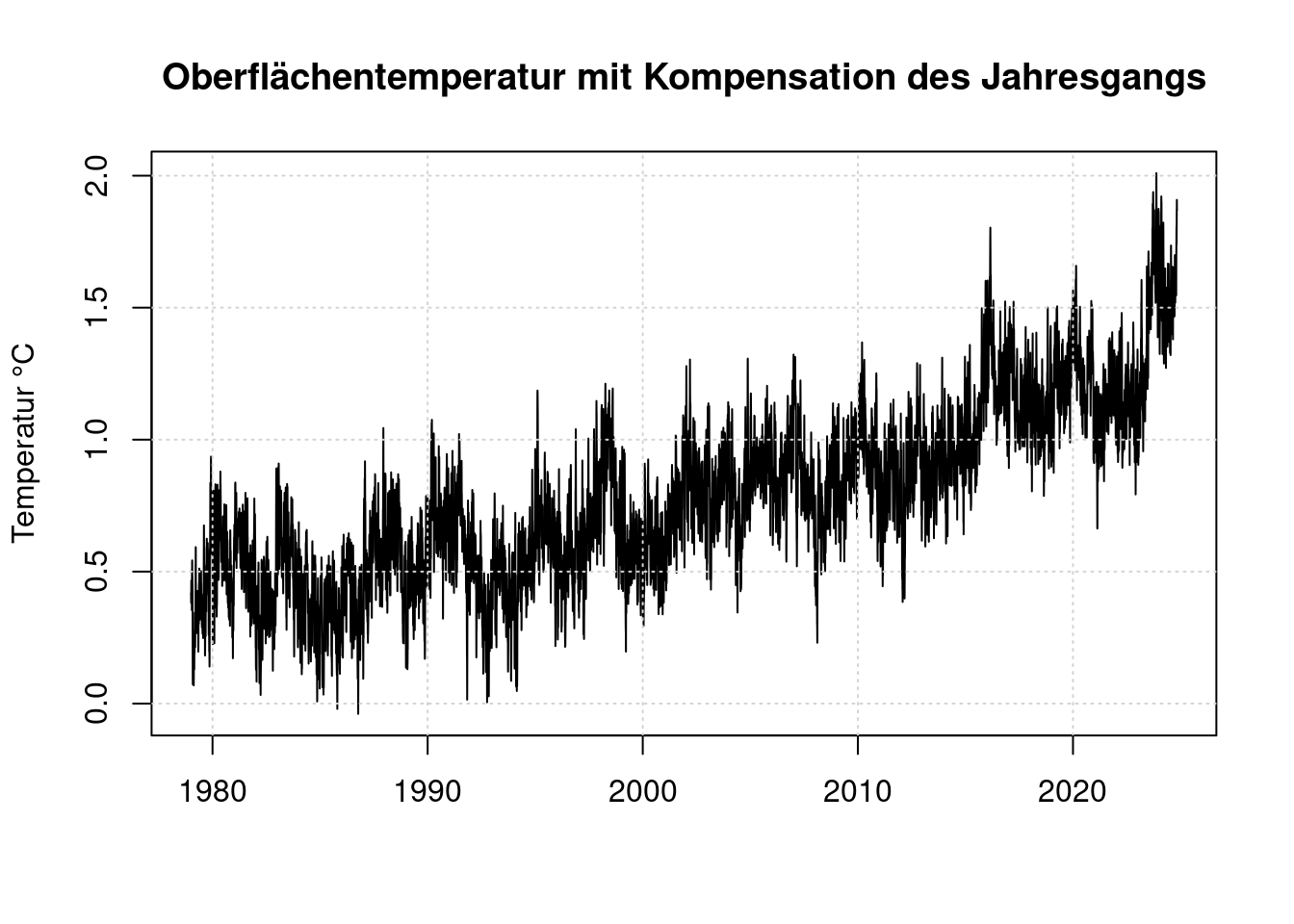

Zunächst ist es nicht überraschend, dass bei stetig steigendem CO2-Anteil in der Atmosphäre die Temperatur stetig steigt. Es fällt auf, dass der Temperaturanstieg 2023 sehr ähnlich aussieht, wie der Temperaturanstieg von 1998:

par(mfcol=c(1, 2));
plot(t, anomaly, xlim=c(1996+0.3,1998+0.3), type='l', ylab='', xlab='', ylim=c(0.8-0.6,2.0-0.6));
plot(t, anomaly, xlim=c(2022    ,2024    ), type='l', ylab='', xlab='', ylim=c(0.8    ,2.0))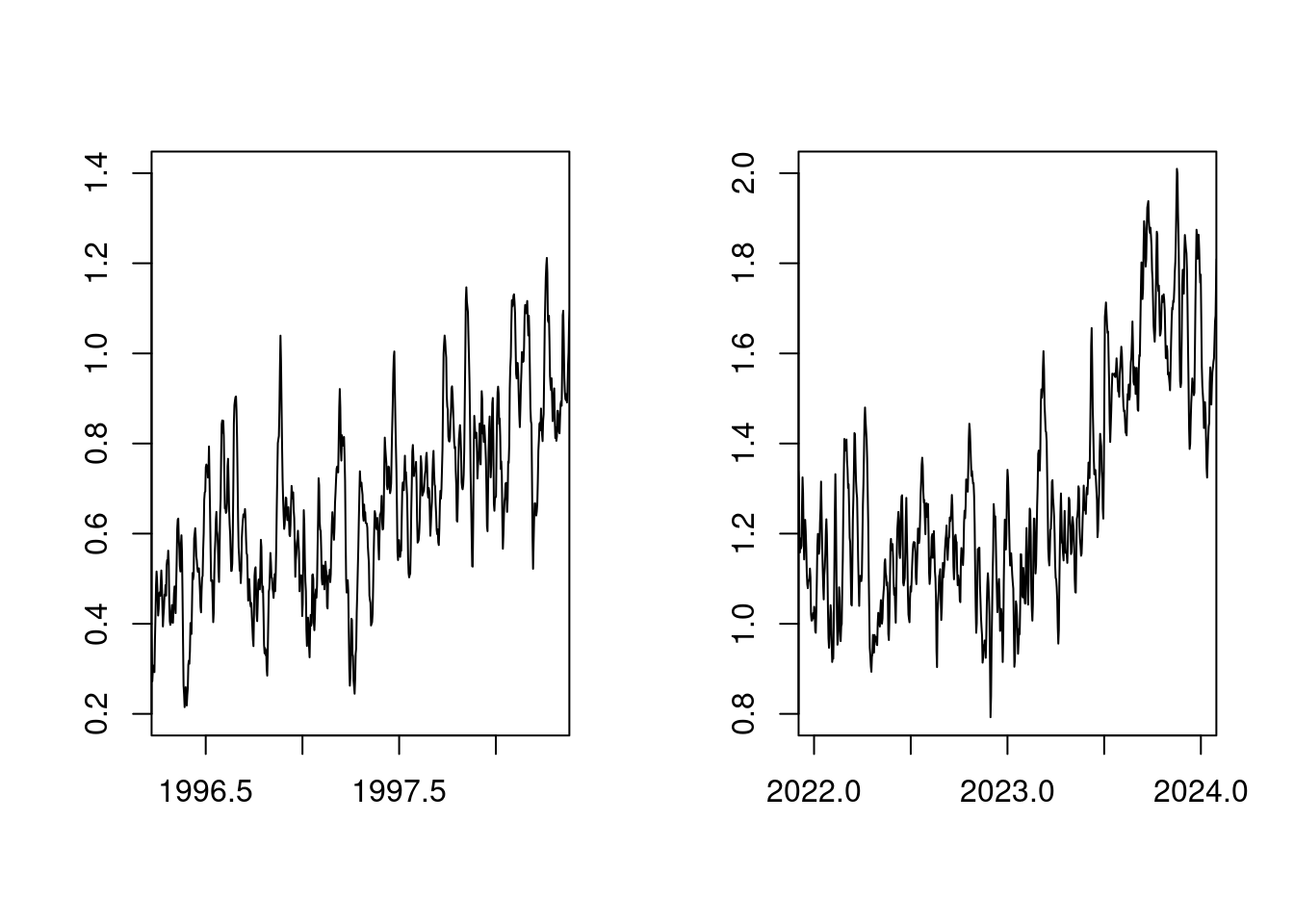

par(mfcol=c(1,1));

Die Ursache hierfür ist, dass sowohl 1998, als auch 2023 Jahre mit einem Starken ENSO (El Niño Southern Oscillation) waren.

7 ENSO

Seit 1979 gibt es Zeitreihenaufzeichnungen zum Status der El Niño Southern Oscilation. Wir laden diese herunter von: https://psl.noaa.gov/enso/mei/data/meiv2.data

Danach bilden wir daraus wieder eine Zeitreihe mit Tagen ab 1979.

raw_enso <- read.table(pipe("tail --lines=+2 meiv2.data|egrep '^19|^20'"),
                       sep="", header=F);
raw_enso$year <- raw_enso$V1; raw_enso$V1 <- NULL;

enso <- 1;

i = 1; # raw_enso$year[1] == 1979
n = 1
while (i <= length(raw_enso$year))
{
    enso[n:(n+30)] <- rep(raw_enso$V2[i], 31); n <- n+31; # Januar
    if ( (raw_enso$year[i] %% 4) == 0 ) {
        enso[n:(n+28)] <- rep(raw_enso$V3[i], 29); n <- n+29; # Februar
    } else {
        enso[n:(n+27)] <- rep(raw_enso$V3[i], 28); n <- n+28; # Februar
    };
    enso[n:(n+30)] <- rep(raw_enso$V4[i], 31); n <- n+31; # März
    enso[n:(n+29)] <- rep(raw_enso$V5[i], 30); n <- n+30; # April
    enso[n:(n+30)] <- rep(raw_enso$V6[i], 31); n <- n+31; # Mai
    enso[n:(n+29)] <- rep(raw_enso$V7[i], 30); n <- n+30; # Juni
    enso[n:(n+30)] <- rep(raw_enso$V8[i], 31); n <- n+31; # Juli
    enso[n:(n+30)] <- rep(raw_enso$V9[i], 31); n <- n+31; # August
    enso[n:(n+29)] <- rep(raw_enso$V10[i], 30); n <- n+30; # September
    enso[n:(n+30)] <- rep(raw_enso$V11[i], 31); n <- n+31; # Oktober
    enso[n:(n+29)] <- rep(raw_enso$V12[i], 30); n <- n+30; # November
    enso[n:(n+30)] <- rep(raw_enso$V13[i], 31); n <- n+31; # Dezember
    i = i+1;
}

# Fill up ENSO Vector if it is shorter
if (length(enso) < length(anomaly)) {
   enso[(length(enso)+1):length(anomaly)] <- enso[length(enso)]
}

enso <- enso[ 1:(length(anomaly)) ];

# The last enso record might only contain data for one month. Fill up with last valid information
i <- length(anomaly)-366;
while (i<=length(anomaly)) {
   if (enso[i] <= -998)
   {
       enso[i] <- enso[i-1];
   }
   i <- i+1;
}

plot(t, enso, main='El Niño Southern Oscillation Index', type='l');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))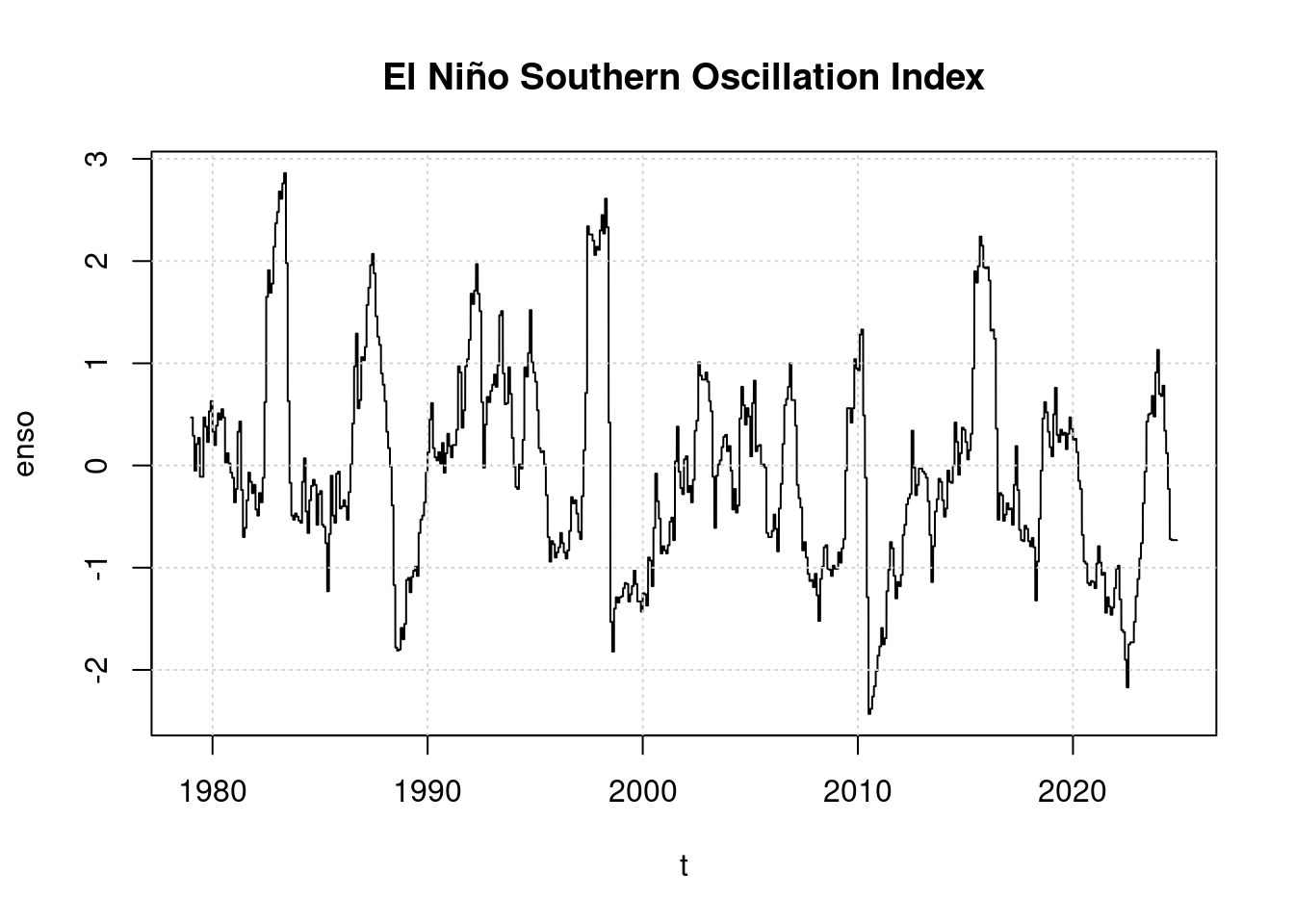

Bemerkenswert ist, dass sich 2023 ein El Niño zu entwickeln beginnt, der Index ist bislang aber nur leicht positiv, weit niedriger als 2016 oder gar 1998. Daher wurde 2023 von Wissenschaftlern nicht als El Niño Jahr eingestuft.

8 CO2

Die Veränderung des CO2-Gehalts in der Atmosphäre laden wir von ftp://ftp.cmdl.noaa.gov/ccg/co2/trends/co2_weekly_mlo.csv Die Datei enthält wöchentliche Angaben der auf Mauna Loa gemessenen CO2-Konzentration. Es gibt Lücken in der Aufzeichnung, die wir bei der Umwandlung in eine Zeitreihe auffüllen müssen.

co2_weekly <- read.table(pipe("grep -v '^#' co2_weekly_mlo.csv"), sep=",", header=T);
co2 <- rep(0,8);
i <- 1;
n <- 1;

while (i <= length(co2_weekly$decimal))
{
    if (co2_weekly$decimal[i] > 1979)
    {
        x <- (co2_weekly$decimal[i] - 1979) * 365.25;
        if (co2_weekly$average[i]>0) {
            co2[x:(x+7)] = rep(co2_weekly$average[i], 8);
        } else {
            co2[x:(x+7)] = rep(co2[length(co2)], 8);
        }
    }
    
    i = i+1;
}

co2[1:6] <- rep(co2[7],6);
if (length(co2) < length(anomaly)) {
  co2[length(co2):length(anomaly)] <- co2[length(co2)];
} else {
   co2 <- co2[1:(length(anomaly))];
}
plot(t, co2, main='CO~2~ Konzentration in Parts per Million', type='l');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))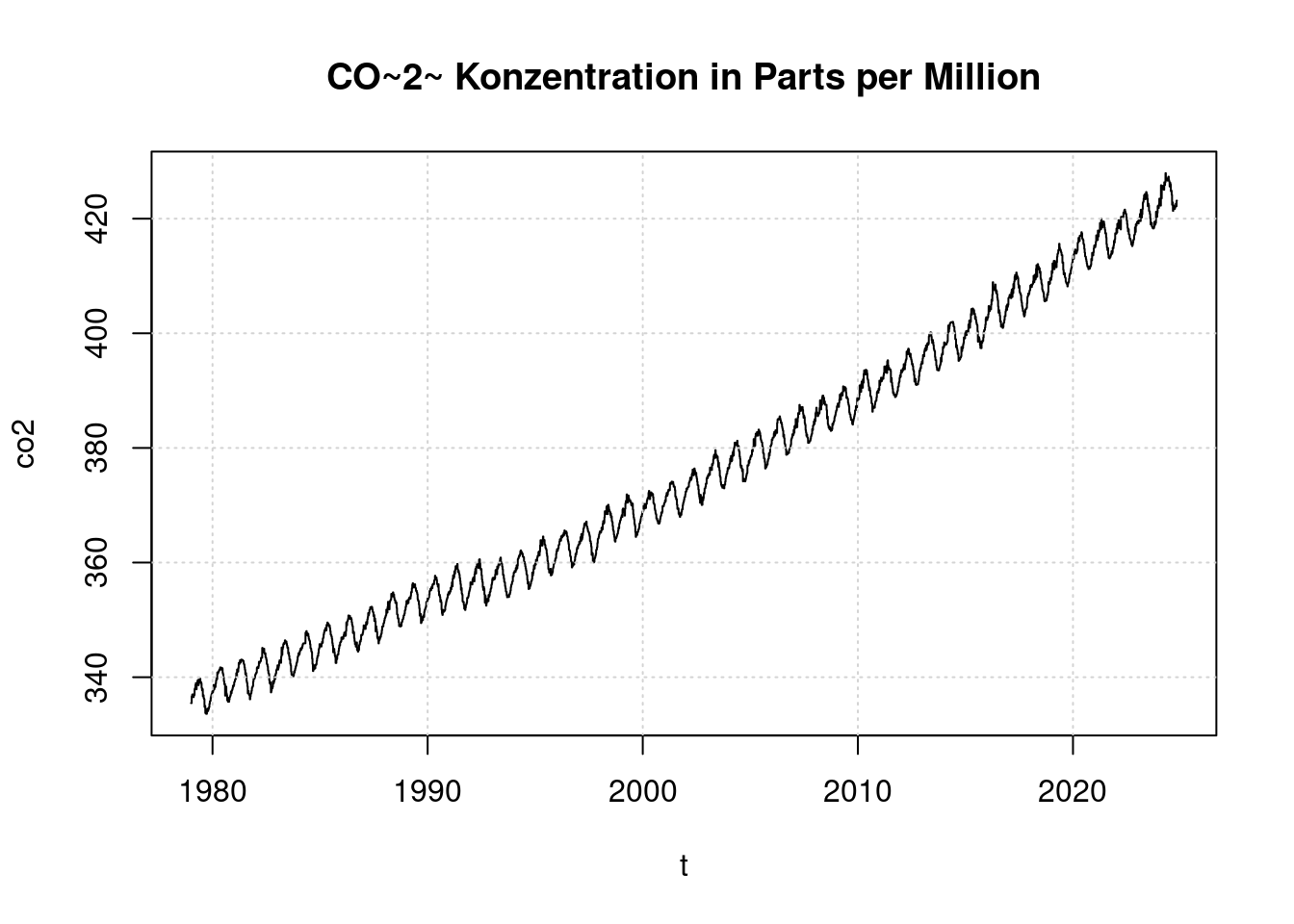

9 Sonnenaktivität

Ein weiterer bekannter Einflußfaktor auf die Erdtemperatur ist die Sonnenaktivität, die typischerweise in ihrer Stärke einen 11-Jährigen Zyklus aufweist. Die Sonnenaktivität kann anhand der Anzahl von Sonnenflecken grob abgeschätzt werdem

Wir laden diese Daten von http://www.sidc.be/silso/DATA/SN_y_tot_V2.0.txt und wandeln sie in eine tagesweise Zeitreihe um.

library(interp);
sun_yearly <- read.table(pipe("sed 's/\\*$//' SN_y_tot_V2.0.txt"), sep="", header=F);
sun_yearly$year <- sun_yearly$V1;  sun_yearly$V1<-NULL;
sun_yearly$sunspots <- sun_yearly$V2;  sun_yearly$V2<-NULL;

sunspots <- aspline((1979-sun_yearly$year[1]+1):(length(sun_yearly$year)), sun_yearly$sunspots[280:(length(sun_yearly$year))], n=length(anomaly))$y;
plot(t, sunspots, main='Anzahl Sonnenflecken', type='l', lwd=3);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))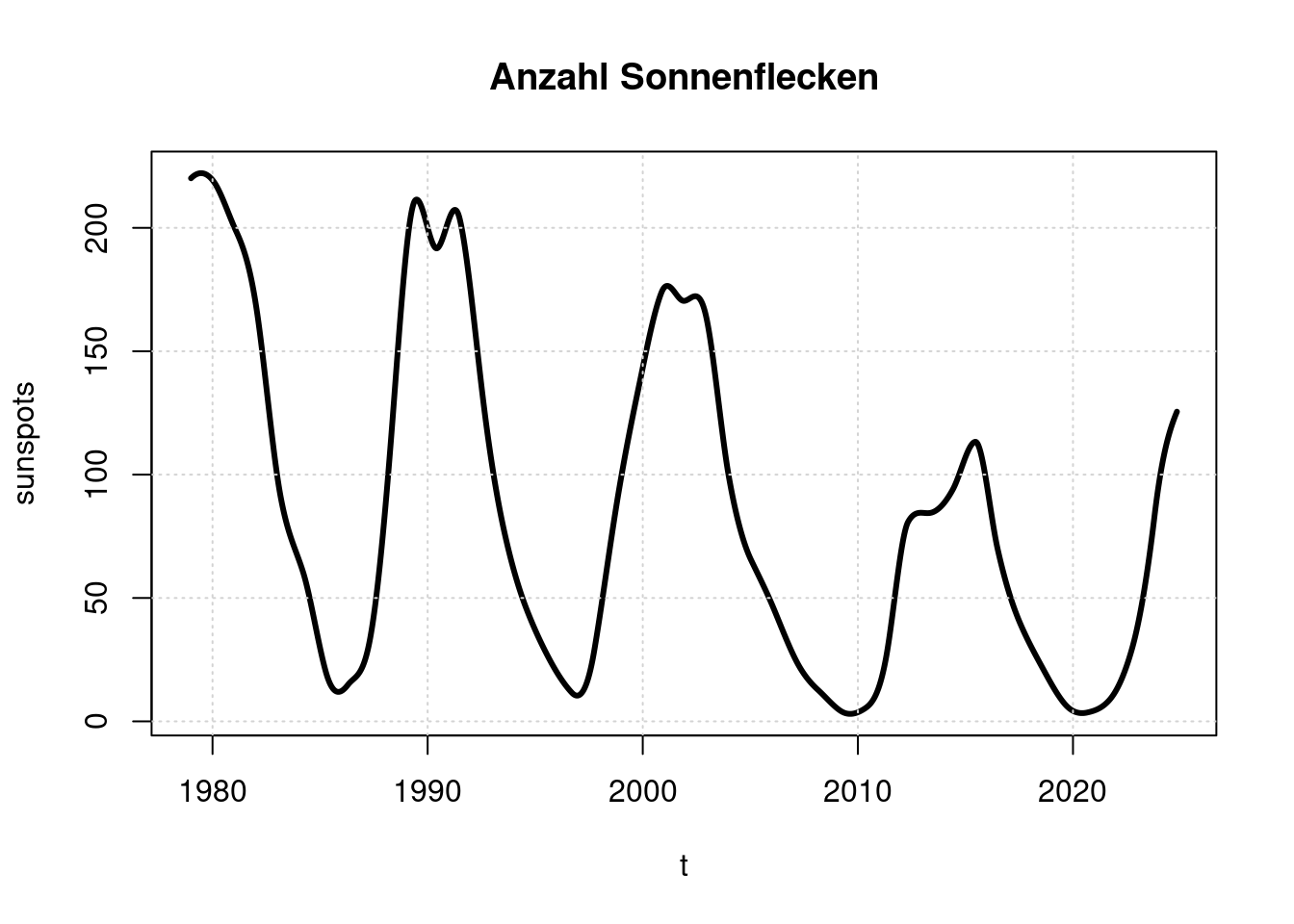

10 Gegenüberstellung

Zur Gegenüberstellung der Einflussgrößen wandeln wir die Daten in einen data.frame um und benutzen xyplot aus dem Lattice Paket. Die gewählten Faktoren sind zunächst absolut willkürlich.

library(lattice);
df <- data.frame(t, anomaly, enso, co2, sunspots)
xyplot(anomaly+enso*0.1+(log(co2/280)-0.1)*4+(sunspots*0.001)~t, data = df, ylab='',
       main = 'Gegenüberstellung der Einflussgrößen', type='l', auto.key=TRUE);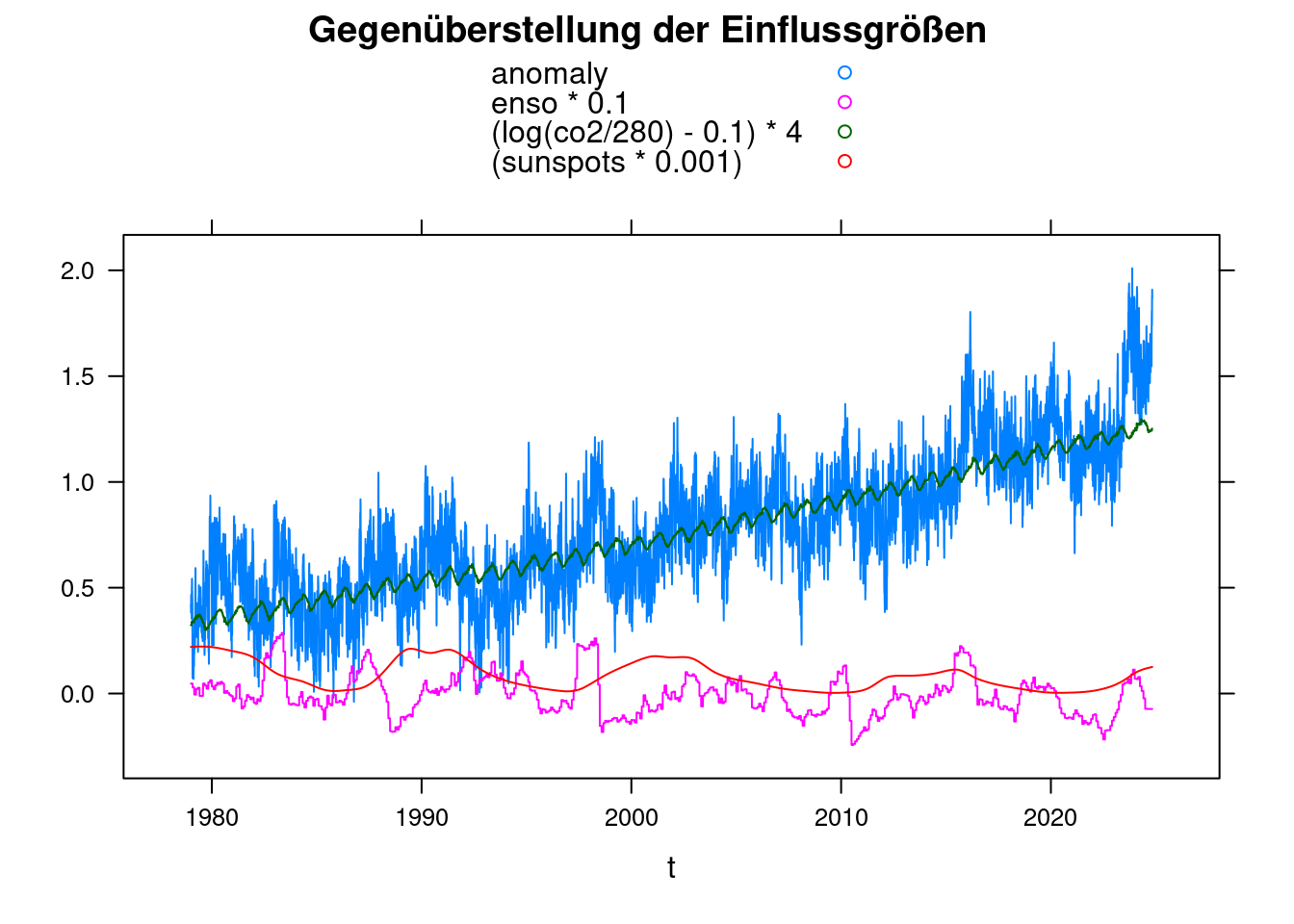

11 Parameter eines Modells

Um zu erkennen, ob es 2023 einen unbekannten Einflußfaktor für die Meeresmitteltemperatur gegeben hat, bestimmen wir mit einem mathematischen Modell, wie gut sich die gemessenen Temperaturen aus den bereits bekannten Einflußgrößen ableiten lassen.

Die Abhängigkeit der Temperatur vom CO2-Gehalt der Atmosphäre modellieren wir logarithmisch, weil die Wärmeveränderung näherungsweise logarithmisch mit dem CO2-Gehalt steigt. Eine Verdopplung des CO2-Gehalts von 280 auf 560ppm verursacht also dieselbe Erwärmung wie eine Verdopplung von 580 auf 1260ppm.

tfit <- nls(anomaly ~ A + B*log(co2/280) + C*enso +D*sunspots, data = df,
            start = list( A=mean(df$anomaly), B=0.01, C=0, D=0) );
tfit;
## Nonlinear regression model
##   model: anomaly ~ A + B * log(co2/280) + C * enso + D * sunspots
##    data: df
##          A          B          C          D 
## -0.5888215  4.5562577  0.0582692  0.0005889 
##  residual sum-of-squares: 504.8
## 
## Number of iterations to convergence: 1 
## Achieved convergence tolerance: 1.348e-07
plot(df$t, df$anomaly, type='l', col='blue', lwd=1, xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
lines(predict(tfit) ~ df$t, type='l', col="darkgreen", lwd=3);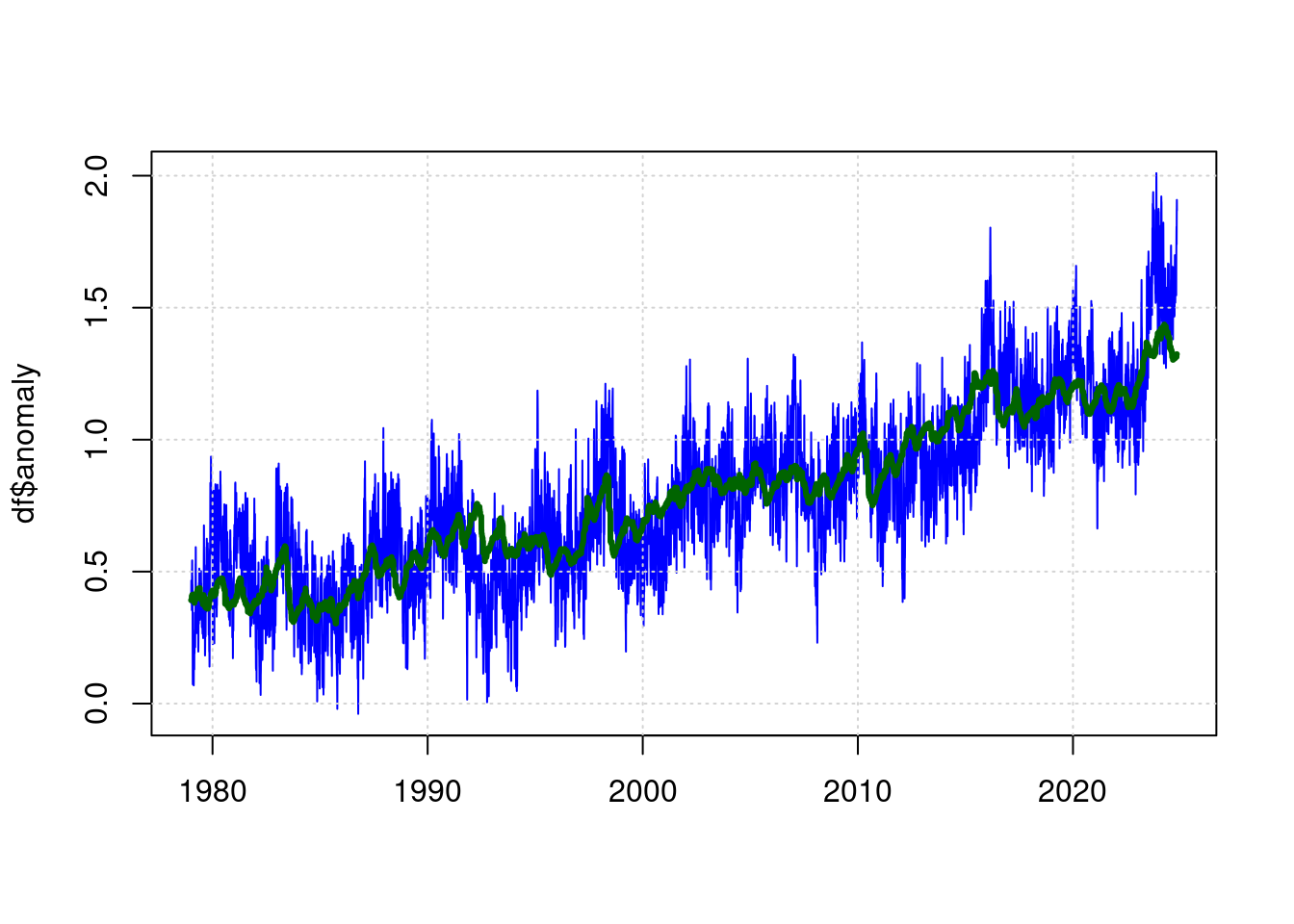

#prediction<-coef(tfit)[1]+coef(tfit)[2]*log(co2/280)+coef(tfit)[3]*enso+coef(tfit)[4]*sunspots;
#lines(prediction ~ df$t, type='l', col="darkgreen", lwd=3);

Die grüne Linie ist nun der Schätzwert für die erwartete Temperatur anhand der Parameter (CO2, ENSO, Sunspots) und die Blaue Linie ist die gemessene Temperatur.

12 Filterung

Es zeigt sich, dass eine Tiefpass-Filterung der Werte von ENSO und CO2 as Modell noch ein wenig verbessert. Der Wert “residual sum-of-squares” im NLS-Ergebnis wird dadurch kleiner.

Zur Filterung verwenden wir einen einfachen IIR-Filter (Infinite-Impulse-Response):

lowpass <- function(inp, lambda) {

value <- mean(inp[1:10]);
result <- 0;
i <- 1;
while (i<=length(inp))
{
    value = value*(1-lambda) + inp[i]*lambda;
    result[i] = value;
    i = i+1;
}

result;
}

Jetzt ergänzen wir gefilterte Werte für enso und co2 im Dataframe df:

df$fco2 <- lowpass(df$co2, 0.012);
df$fenso <- lowpass(df$enso, 0.012);

# Verschiebung von ENSO um 40 Tage, d.h. Wirkung ist 40 Tage später als Ursache
df$fenso <-c( rep(0, 40),
              df$fenso[ 1:(length(df$fenso)-40) ]
            );

Und wir aktualisieren unser Modell:

ffit <- nls(anomaly ~ A + B*log(fco2/280) + C*fenso +D*sunspots, data = df,
            start = list( A=mean(df$anomaly), B=0.01, C=0, D=0) );
ffit;
## Nonlinear regression model
##   model: anomaly ~ A + B * log(fco2/280) + C * fenso + D * sunspots
##    data: df
##          A          B          C          D 
## -0.6329042  4.7128437  0.0880975  0.0006484 
##  residual sum-of-squares: 462.6
## 
## Number of iterations to convergence: 1 
## Achieved convergence tolerance: 1.139e-07
plot(df$t, df$anomaly, type='l', col='blue', lwd=1);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
lines(predict(ffit) ~ df$t, type='l', col="darkgreen", lwd=3);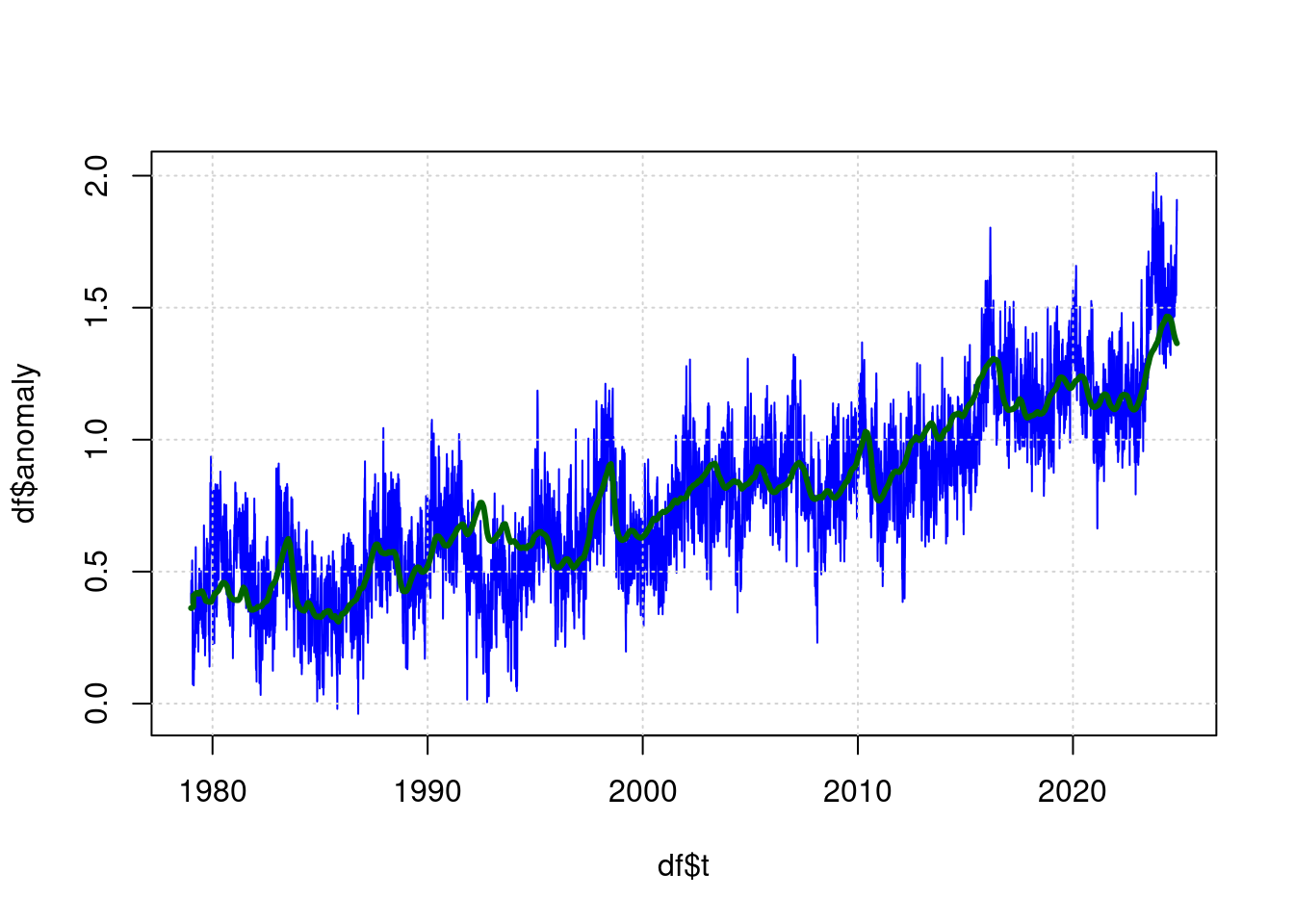

#prediction<-coef(ffit)[1]+coef(ffit)[2]*log(co2/280)+coef(ffit)[3]*enso+coef(ffit)[4]*sunspots;
#lines(prediction ~ df$t, type='l', col="darkgreen", lwd=3);

13 Das Residuum

Der Teil des Messergebnisses, der nach dem Modell nicht aus den Eingangswerten abgeleitet werden kann, sieht damit so aus:

residuum <- anomaly - predict(ffit);
plot(df$t, residuum, type='l', col='blue', lwd=1);
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))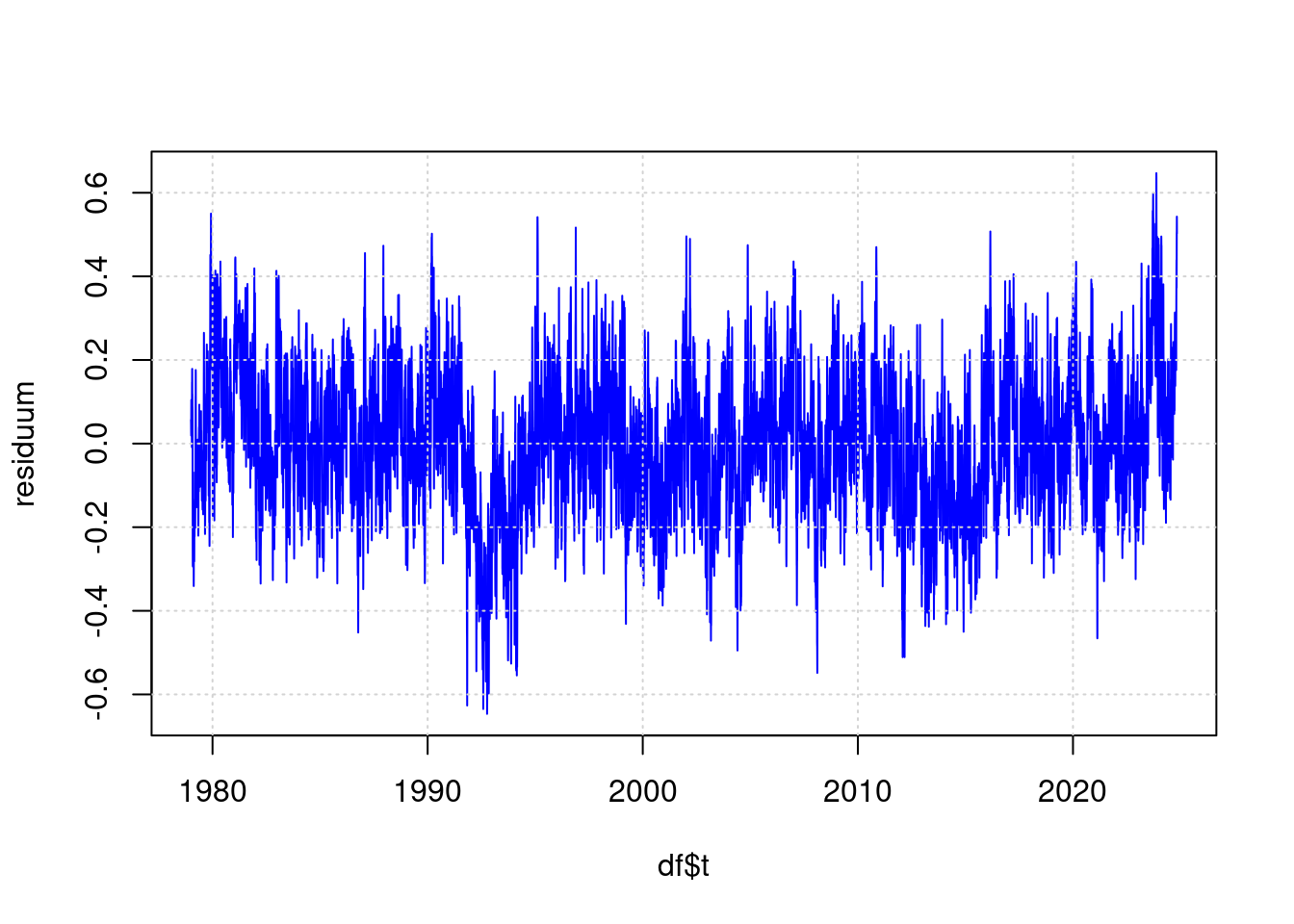

Das ist also der Teil der Messung, der nicht aus CO2, ENSO und Sonnenflecken hergeleitet werden kann. Hier sieht das hohe Messergebnis von 2023 bei weitem nicht mehr so beeindruckend aus wie in der ursprünglichen Visualisierung.

14 Gegenüberstellung

fval<-coef(ffit);
xyplot(anomaly+(log(fco2/280)*fval[2]+fval[1])+fenso*fval[3]+sunspots*fval[4]~t, data = df,
       xlab='', ylab='Temperatur °C',
       main = 'Gegenüberstellung Einflußgrößen', type='l', auto.key=TRUE);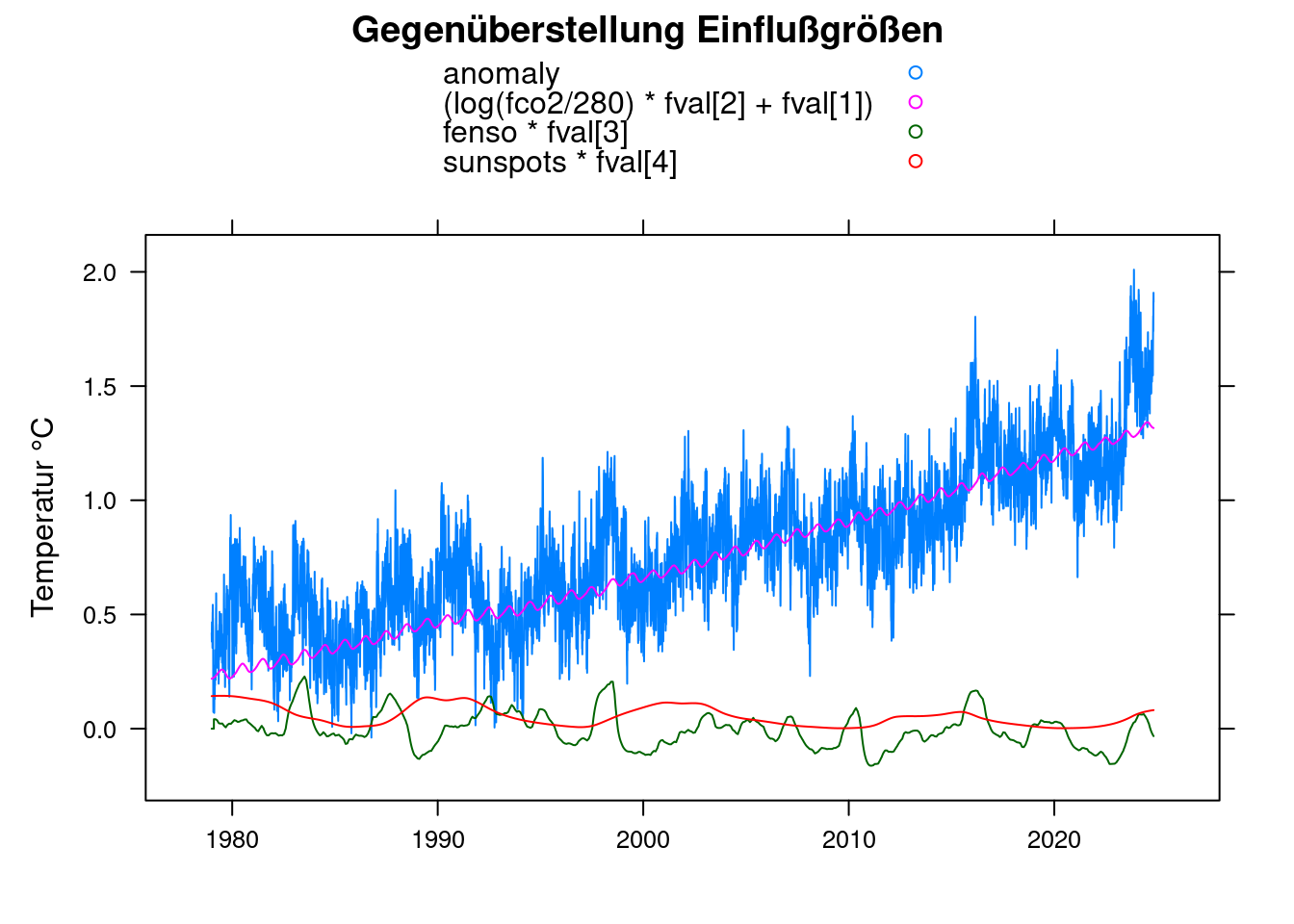

15 Tagesrauschen ausfiltern

Da das Rauschen den Plot schwer erkennbar macht, wenden wir die Tiefpassfilterung noch auf die Messwerte “anomalie” an, um einen glatteren Plot zu erhalten:

df$fanomaly <- lowpass(df$anomaly, 0.025);
xyplot(fanomaly+(log(fco2/280)*fval[2]+fval[1])+fenso*fval[3]+sunspots*fval[4]~t, data = df,
       main = 'Gegenüberstellung Einflußgrößen', type='l', auto.key=TRUE,
       ylab = 'Temperatur °C', xlab='');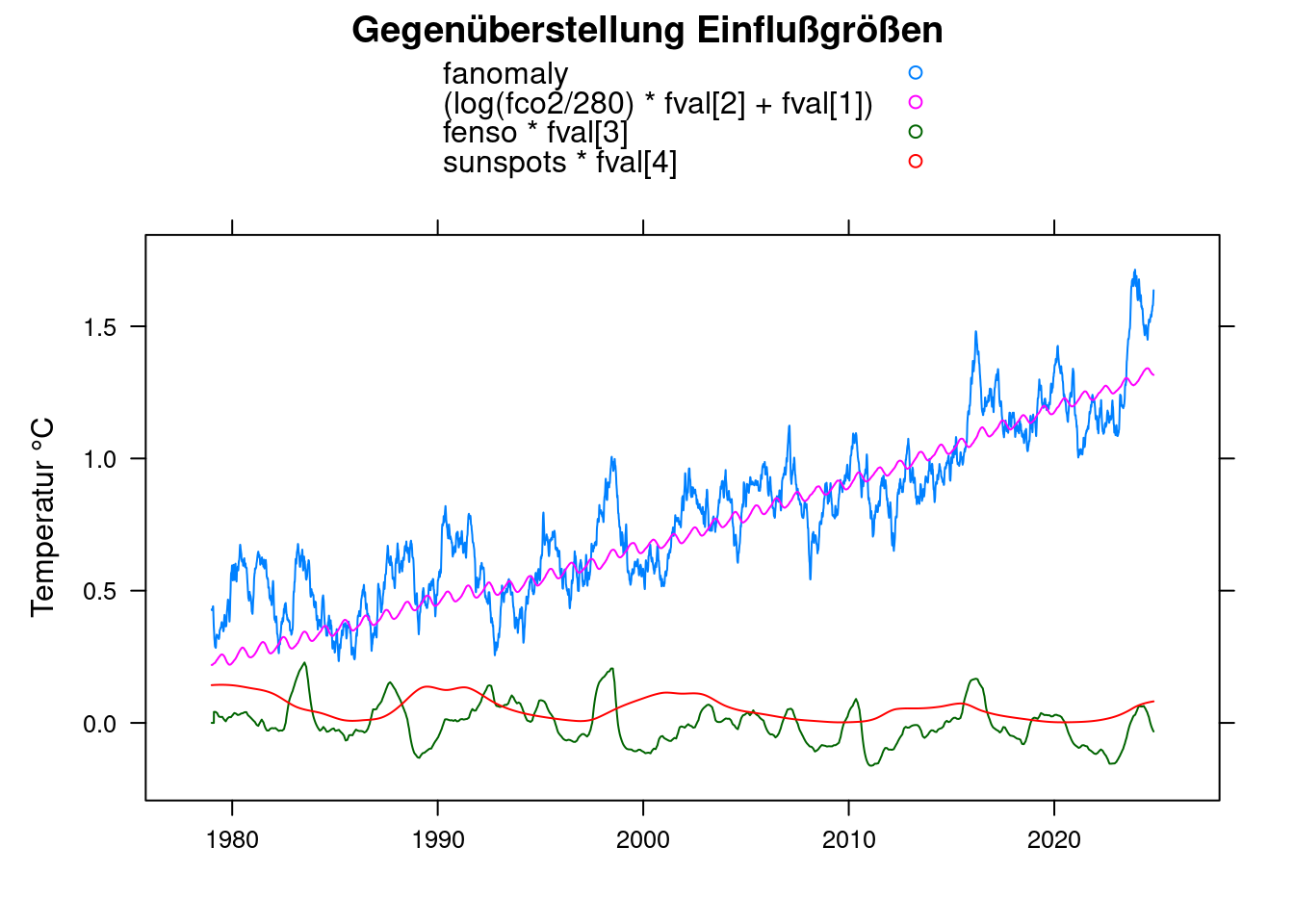

Dasselbe für das Residuum

fresiduum <- lowpass(residuum, 0.025);
plot(df$t, fresiduum, type='l', col='blue', lwd=1, xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))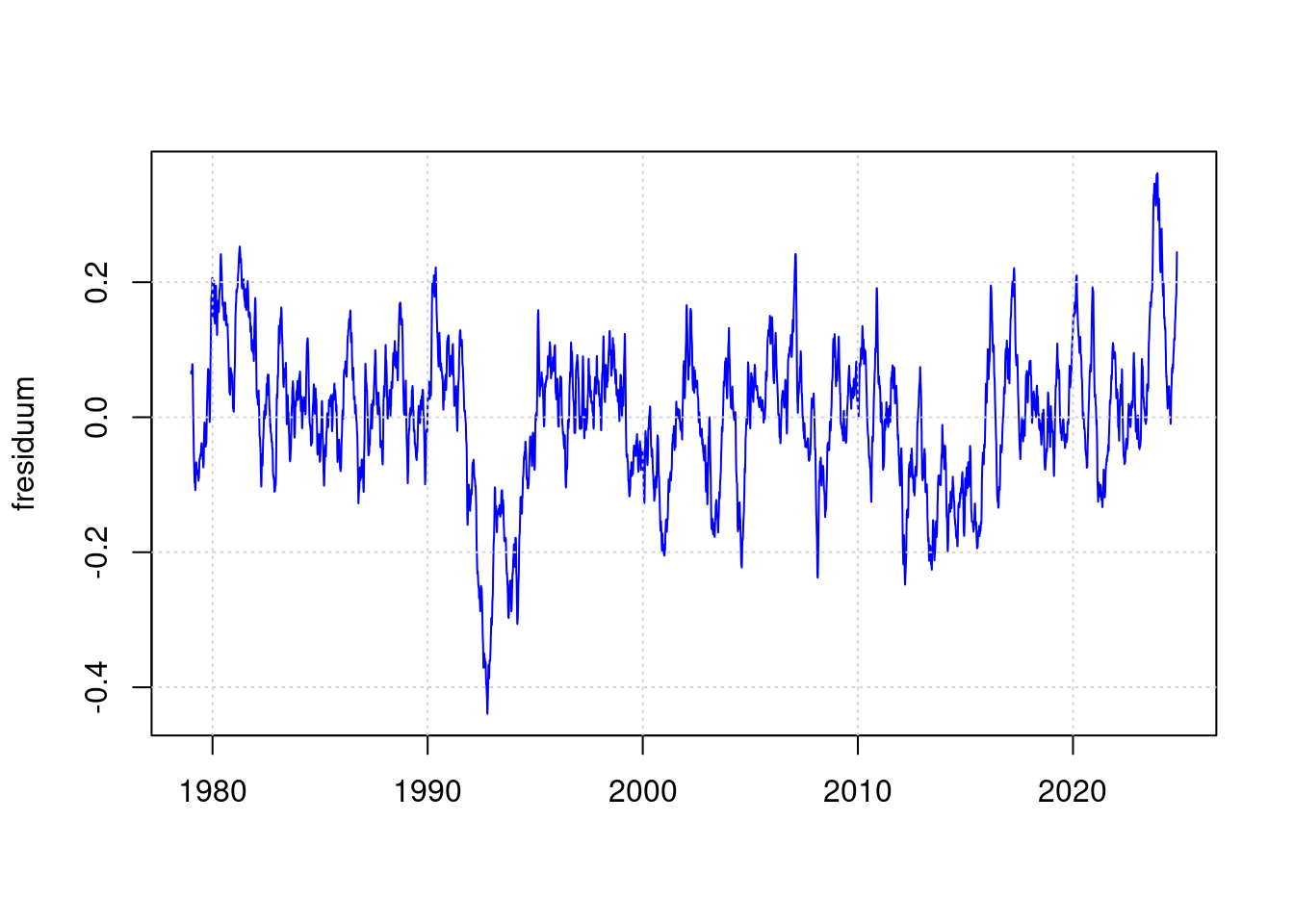

Die Auffäligkeit von 2023 sieht damit schon nicht mehr so beeindruckend aus.

16 Berücksichtigung der Vulkanexplosition Mount Pinatubo

Viel Auffälliger ist im Residuum der starke Abfall der Temperatur gegen 1992. Die Ursache hierfür ist bekannt: Der Vulkan Mount Pinatubo ist explodiert und seine Emissionen haben die Erde damals abgekühlt. James Hansen hat damals diese Abkühlung als Folge der Explosion korrekt vorhergesagt:

Die Daten sind eine grobe Verssion des Plots aus dem Hansen-Paper von 1991.

y <- 0:8 * 0.42 + 1991.5;
raw_pinatubo <- c(0, 1.7, 4.5, 3, 2, 1.5, 1, 0.4, 0);
npinatubo <- as.integer((y[length(y)]-y[1]+1) * 365.25);
spinatubo <- as.integer( ((1991.5-1979)*365.25 ) )+1;
pinatubo <- rep(0, length(anomaly));
pinatubo[spinatubo:(spinatubo+npinatubo-1)] <- aspline(y, raw_pinatubo, n=npinatubo)$y;
df$pinatubo <- pinatubo;

pfit <- nls(anomaly ~ A + B*log(fco2/280) + C*fenso +D*sunspots + E*pinatubo, data = df,
            start = list( A=mean(df$anomaly), B=0.01, C=0, D=0, E=-0.01) );
pfit;
## Nonlinear regression model
##   model: anomaly ~ A + B * log(fco2/280) + C * fenso + D * sunspots +     E * pinatubo
##    data: df
##          A          B          C          D          E 
## -0.5879655  4.6146407  0.1060431  0.0006422 -0.0896742 
##  residual sum-of-squares: 408.9
## 
## Number of iterations to convergence: 1 
## Achieved convergence tolerance: 1.887e-07
pval <- coef(pfit);

xyplot(fanomaly+(log(fco2/280)*pval[2]+pval[1])+fenso*pval[3]+sunspots*pval[4]+pinatubo*pval[5]~t, data = df,
       main = 'Gegenüberstellung Einflußgrößen', type='l', auto.key=TRUE,
       ylab = 'Temperatur °C', xlab='');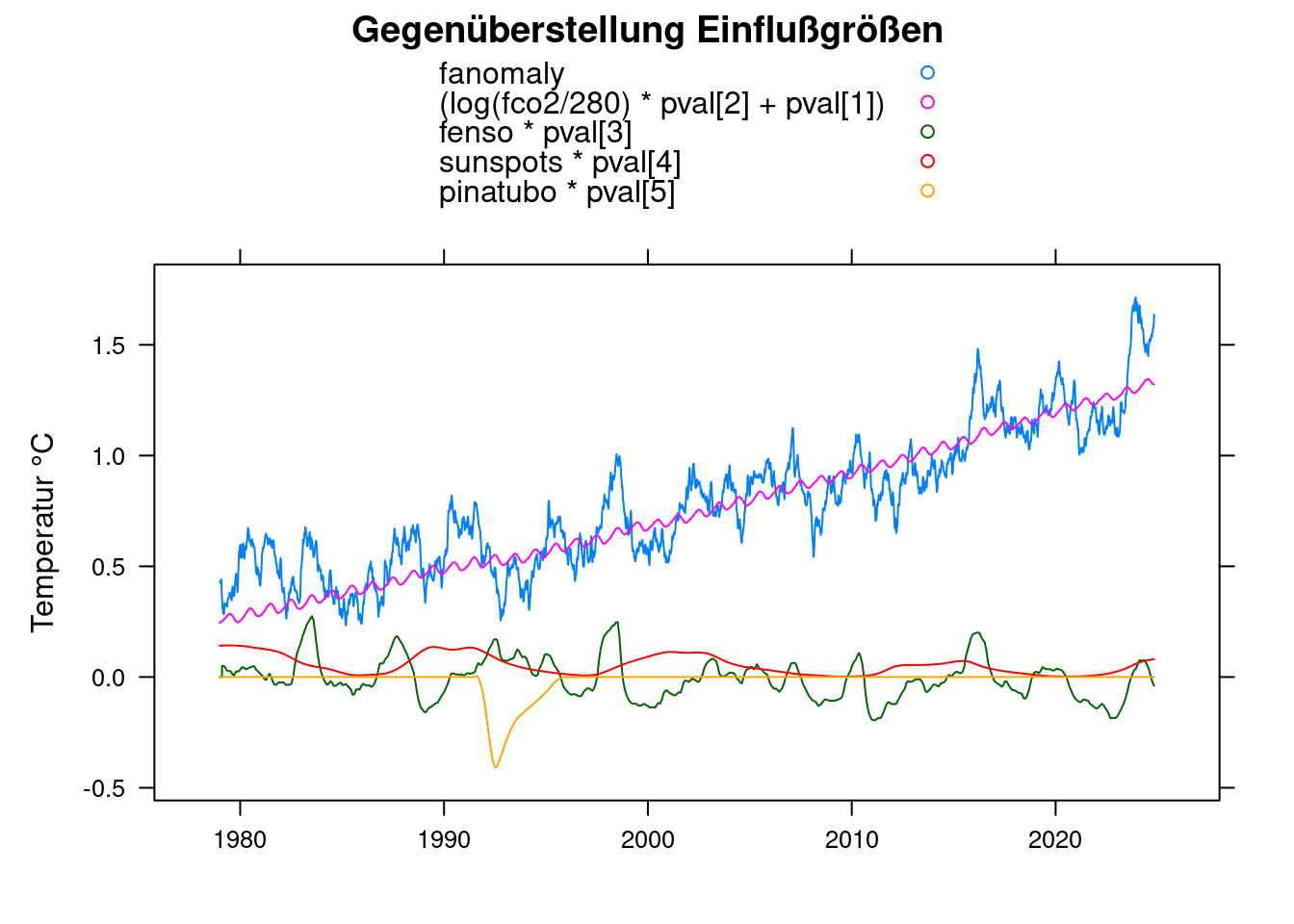

residuum <- anomaly - predict(pfit);
fresiduum <- lowpass(residuum, 0.025);

plot(df$t, fresiduum, type='l', col='blue', lwd=1,
     xlab='', ylab='°C', main='Residuum gefiltert mit Mount Pinatubo');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))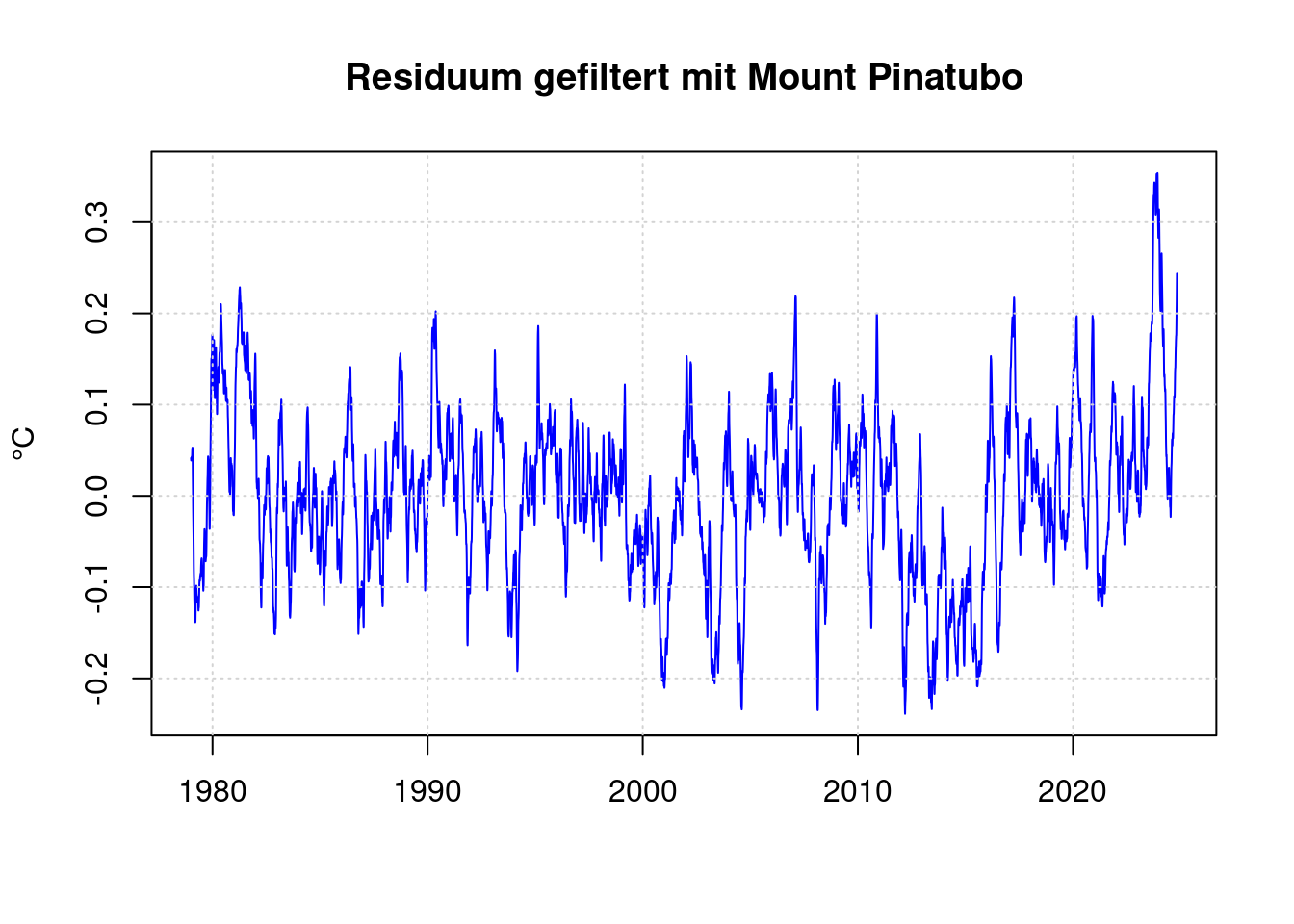

17 Statistik

Die Standardabweichung des Residuums beträgt:

standard_deviation = sd(residuum);
standard_deviation;
## [1] 0.1562938

Der höchste Wert des Residuums beträgt damit in Standardabweichungen (Sigma):

max(residuum / standard_deviation);
## [1] 4.073982
min(residuum / standard_deviation);
## [1] -3.910879

Die Wahrscheinlichkeit, dass ein Wert in einer Meßreihe diesen Wert erreicht, beträgt:

pnorm(-max(residuum)/standard_deviation);
## [1] 2.310805e-05

Das sieht erst mal sehr wenig aus, aber unsere Zeitreihe enthält ja auch Messungen für jeden Tag aus mehreren Jahrzehnten. Dementsprechend ist zu erwarten, dass dieser maximalwert im Mittel an

pnorm(-max(residuum)/standard_deviation) * length(residuum);
## [1] 0.3868518

Tagen erreicht wird.

Ein Wert von +0.5 Grad wurde erreicht an:

sum(residuum > 0.5)
## [1] 29

Tagen.

Zu erwarten sind laut Statistik:

pnorm(-0.5/standard_deviation) * length(residuum);
## [1] 11.53922

Der beobachtete Temperaturtrend beträgt in °C je Jahrzehnt:

plot(df$t, df$fanomaly, type='l', main='After removing seasonal average');

lmAnomaly <- lm(anomaly ~ t)
abline(lmAnomaly);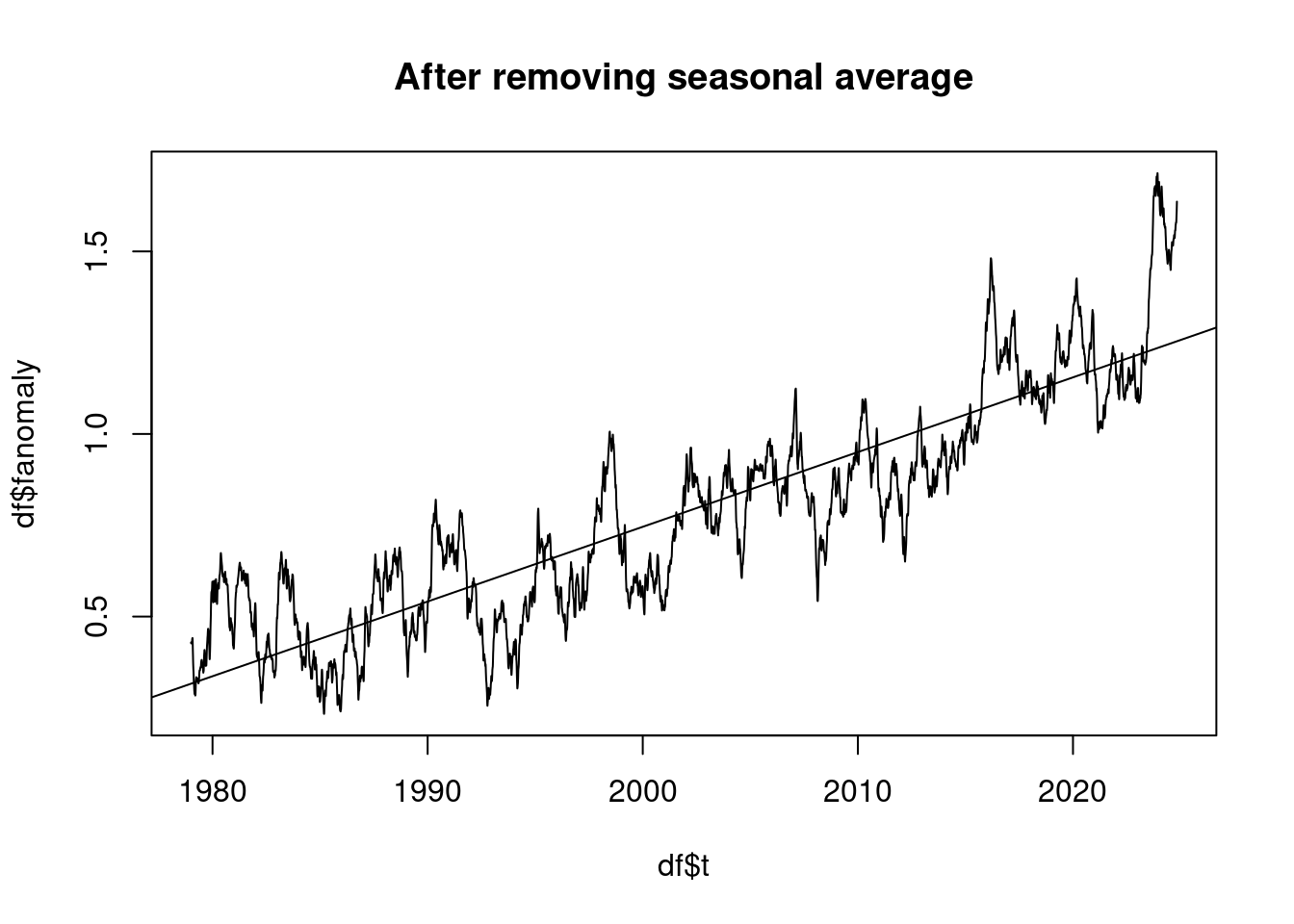

coef(lmAnomaly)[2]*10
##         t 
## 0.2046325

18 Beschleunigt sich die Erwärmung?

Die Arbeit von James Hansen behauptet ja, dass sich die globale Erwärmung in den letzten Jahren beschleunigt hätte, insbesondere seit die weltweiten SO2 Emissionen in den letzten Jahren gesenkt wurden.

Es zeigt sich, dass man je nach gewählten Zeiträumen den Eindruck erwecken kann, die Erwärmung hätte sich wesentlich beschleunigt, oder es habe keine wesentliche Veränderung stattgefunden:

plot_line <- function(dataframe, col) {
lm <- lm(dataframe$anomaly ~ dataframe$t)
co <- coef(lm);
lines(c(dataframe$t[1], dataframe$t[length(dataframe$t)]),
      c(co[1] + co[2] * dataframe$t[1], c(co[1] + co[2] * dataframe$t[length(dataframe$t)])),
      col=col);
print( sprintf("Von %.0f bis %.0f %.2f °C pro Jahrzehnt",
               dataframe$t[1], dataframe$t[length(dataframe$t)], co[2]*10) );
}
plot(df$t, df$fanomaly, type='l', main='Globale Erwärmung erfolgt mit konstanter Geschwindigkeit');
abline(lmAnomaly, col='yellow', lwd=2);
plot_line(subset(df, t>1994 & t<2004), 'green');
## [1] "Von 1994 bis 2004 0.28 °C pro Jahrzehnt"
plot_line(subset(df, t>2004 & t<2024), 'green');
## [1] "Von 2004 bis 2024 0.28 °C pro Jahrzehnt"
plot_line(subset(df, t>2014 & t<2024), 'blue');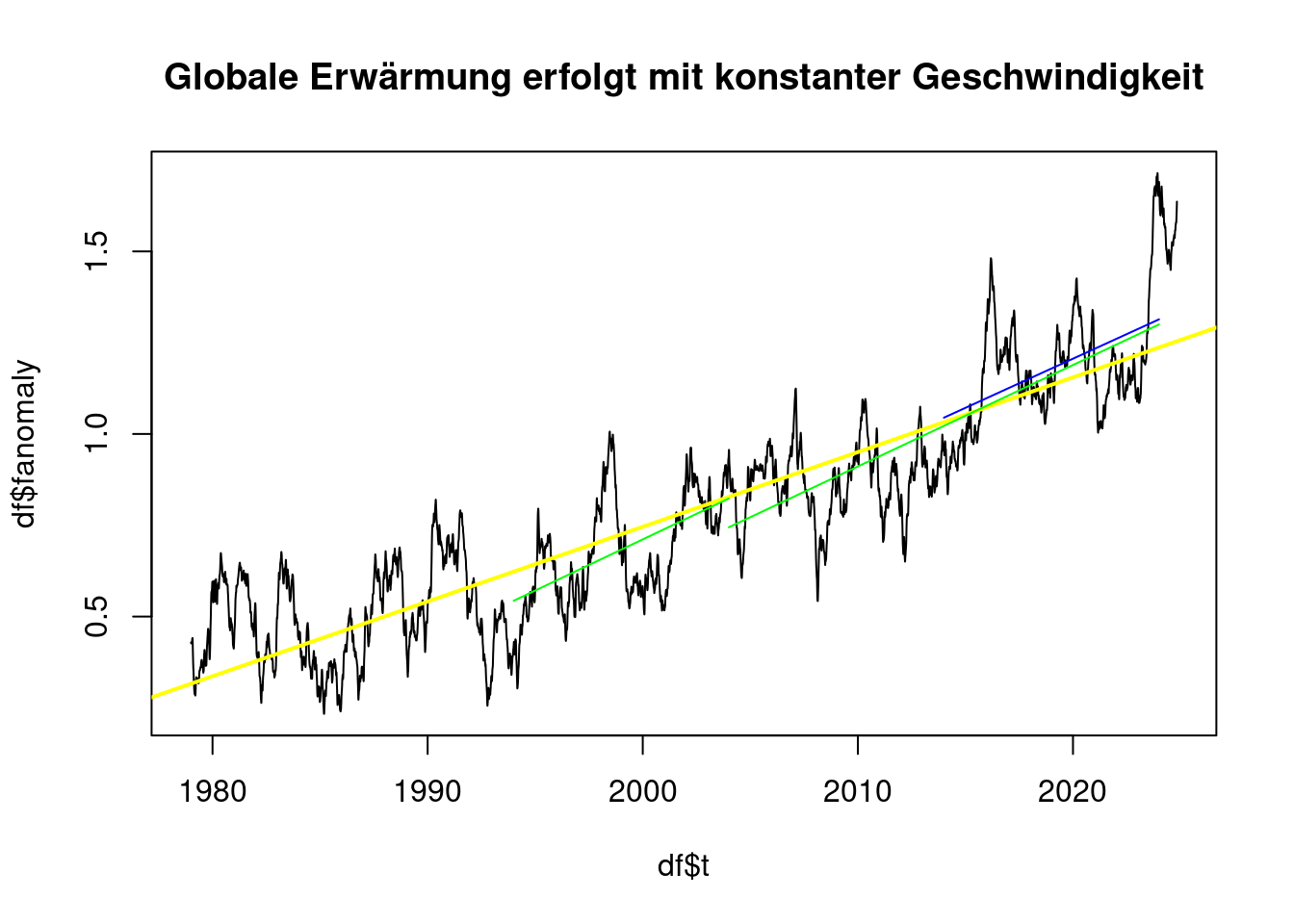

## [1] "Von 2014 bis 2024 0.27 °C pro Jahrzehnt"
plot(df$t, df$fanomaly, type='l', main='Globale Erwärmung beschleunigt sich');
abline(lmAnomaly, col='yellow', lwd=2);
plot_line(subset(df, t<2000), 'red');
## [1] "Von 1979 bis 2000 0.11 °C pro Jahrzehnt"
plot_line(subset(df, t>1990 & t<2010), 'red');
## [1] "Von 1990 bis 2010 0.19 °C pro Jahrzehnt"
plot_line(subset(df, t>2000 & t<2020), 'red');
## [1] "Von 2000 bis 2020 0.25 °C pro Jahrzehnt"
plot_line(subset(df, t>2004 & t<2024), 'red');
## [1] "Von 2004 bis 2024 0.28 °C pro Jahrzehnt"
plot_line(subset(df, t>2010 & t<2024), 'red');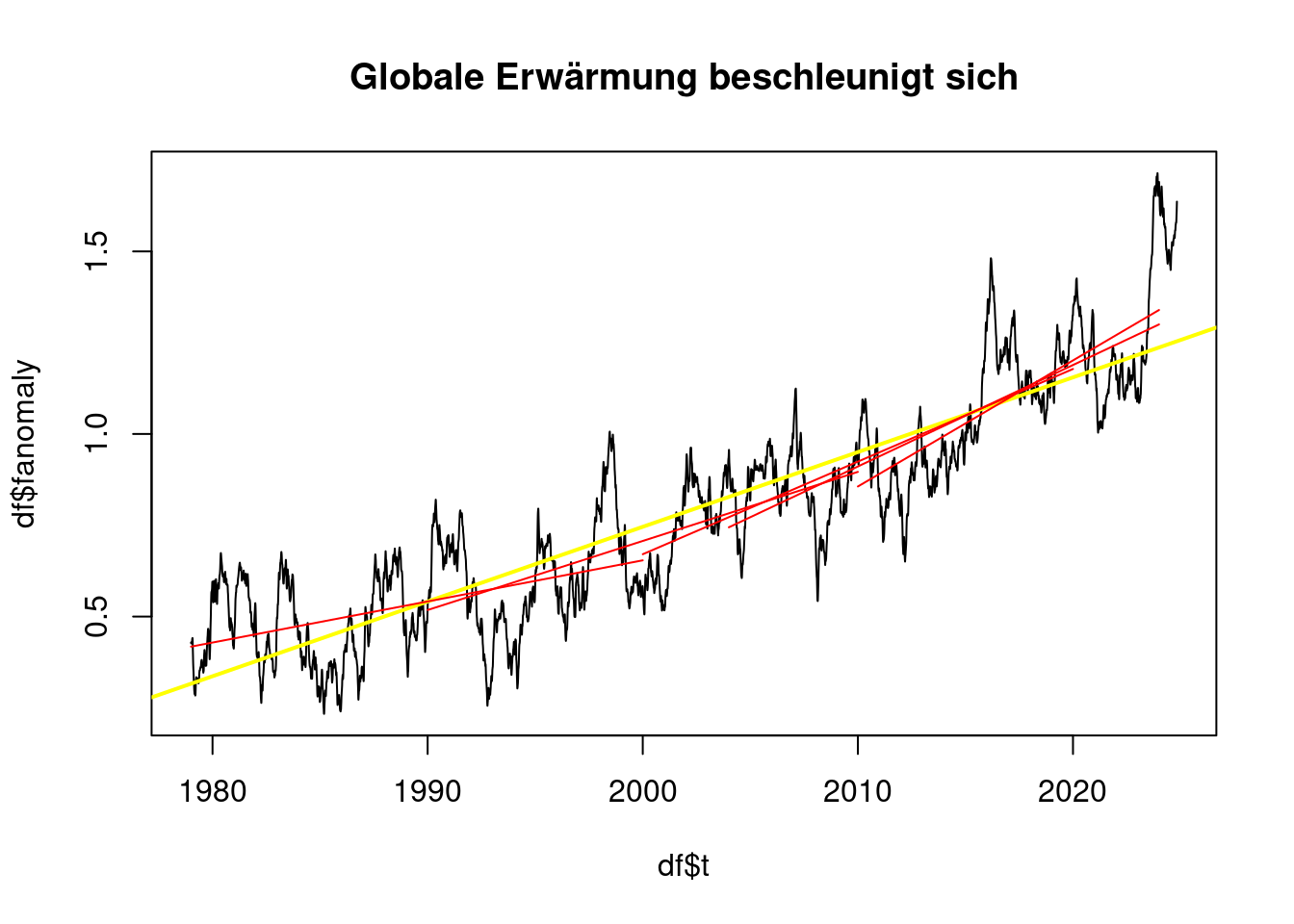

## [1] "Von 2010 bis 2024 0.35 °C pro Jahrzehnt"

Jedoch sind Zeiträume von mehr als 20 Jahren Länge nur unter 0,2°C pro Jahrzehnt, wenn sie sehr früh liegen.

19 Vergleich mit gistemp

Zum Vergleich der climatereanalyzer.org Daten mit den gistemp-Daten der NASA nutzen wir die monatlichen Daten des gistemp-Datensatzes.

Die Daten von Climetereanalyzer.org als Tagesdaten rauschen viel stärker als die monatlichen gistemp-Daten. Um sie vergleichbar zu machen, bilden wir aus ihnen die monatlichen Mittelwerte.

i = 1;
n = 1;
mon_gistemp <- 0;

while (i <= length(giss$year))
{
  if (giss$year[i] >= 1979) {
    mon_gistemp[n] <- giss$jan[i]; n<-n+1;
    mon_gistemp[n] <- giss$feb[i]; n<-n+1;
    mon_gistemp[n] <- giss$mar[i]; n<-n+1;
    mon_gistemp[n] <- giss$apr[i]; n<-n+1;
    mon_gistemp[n] <- giss$may[i]; n<-n+1;
    mon_gistemp[n] <- giss$jun[i]; n<-n+1;
    mon_gistemp[n] <- giss$jul[i]; n<-n+1;
    mon_gistemp[n] <- giss$aug[i]; n<-n+1;
    mon_gistemp[n] <- giss$sep[i]; n<-n+1;
    mon_gistemp[n] <- giss$oct[i]; n<-n+1;
    mon_gistemp[n] <- giss$nov[i]; n<-n+1;
    mon_gistemp[n] <- giss$dec[i]; n<-n+1;
  }
  i = i+1;
}

# Remove NA values from gistemp for incomplete years
if (sum(is.na(mon_gistemp))) {
    gistemp_n <- sum(!is.na(mon_gistemp));
    mon_gistemp <- mon_gistemp[1:gistemp_n];
}

# gistemp data is based on 1951-1980 average, rebase to 1880-1899 average
mon_gistemp <- mon_gistemp - (mean_1880_1899 - mean_1951_1980);

day2mon <- function(daily) {

year <- 1979;
dst <- 1;
mon <- 0;
src <- 1;
while (src < length(daily))
{
    mon[dst] <- mean( daily[src:(src+30)] ); src<-src+31; # Januar
    if ( (year %% 4) == 0 ) {
       mon[dst+1] <- mean( daily[src:(src+28)] ); src<-src+29; # Februar
    } else {
       mon[dst+1] <- mean( daily[src:(src+27)] ); src<-src+28; # Februar
    }
    mon[dst+2] <- mean( daily[src:(src+30)] ); src<-src+31; # März
    mon[dst+3] <- mean( daily[src:(src+29)] ); src<-src+30; # April
    mon[dst+4] <- mean( daily[src:(src+30)] ); src<-src+31; # Mai
    mon[dst+5] <- mean( daily[src:(src+29)] ); src<-src+30; # Juni
    mon[dst+6] <- mean( daily[src:(src+30)] ); src<-src+31; # Juli
    mon[dst+7] <- mean( daily[src:(src+30)] ); src<-src+31; # August
    mon[dst+8] <- mean( daily[src:(src+29)] ); src<-src+30; # September
    mon[dst+9] <- mean( daily[src:(src+30)] ); src<-src+31; # Oktober
    mon[dst+10]<- mean( daily[src:(src+29)] ); src<-src+30; # November
    mon[dst+11]<- mean( daily[src:(src+30)], na.rm=TRUE); src<-src+31; # Dezember
    dst <- dst+12;
    year <- year+1;
}
mon;
}

mon_anomaly <- day2mon(anomaly);
mon_anomaly <- mon_anomaly[1:length(mon_gistemp)];

mon <- 1979 + (0:(length(mon_anomaly)-1)) / 12;
mon = data.frame(mon, mon_anomaly, mon_gistemp);
xyplot(mon_anomaly+mon_gistemp~mon, data = mon, ylab='°C',
       main = 'Gegenüberstellung climatereanalyzer mit gistemp', type=c('l','g'), auto.key=TRUE);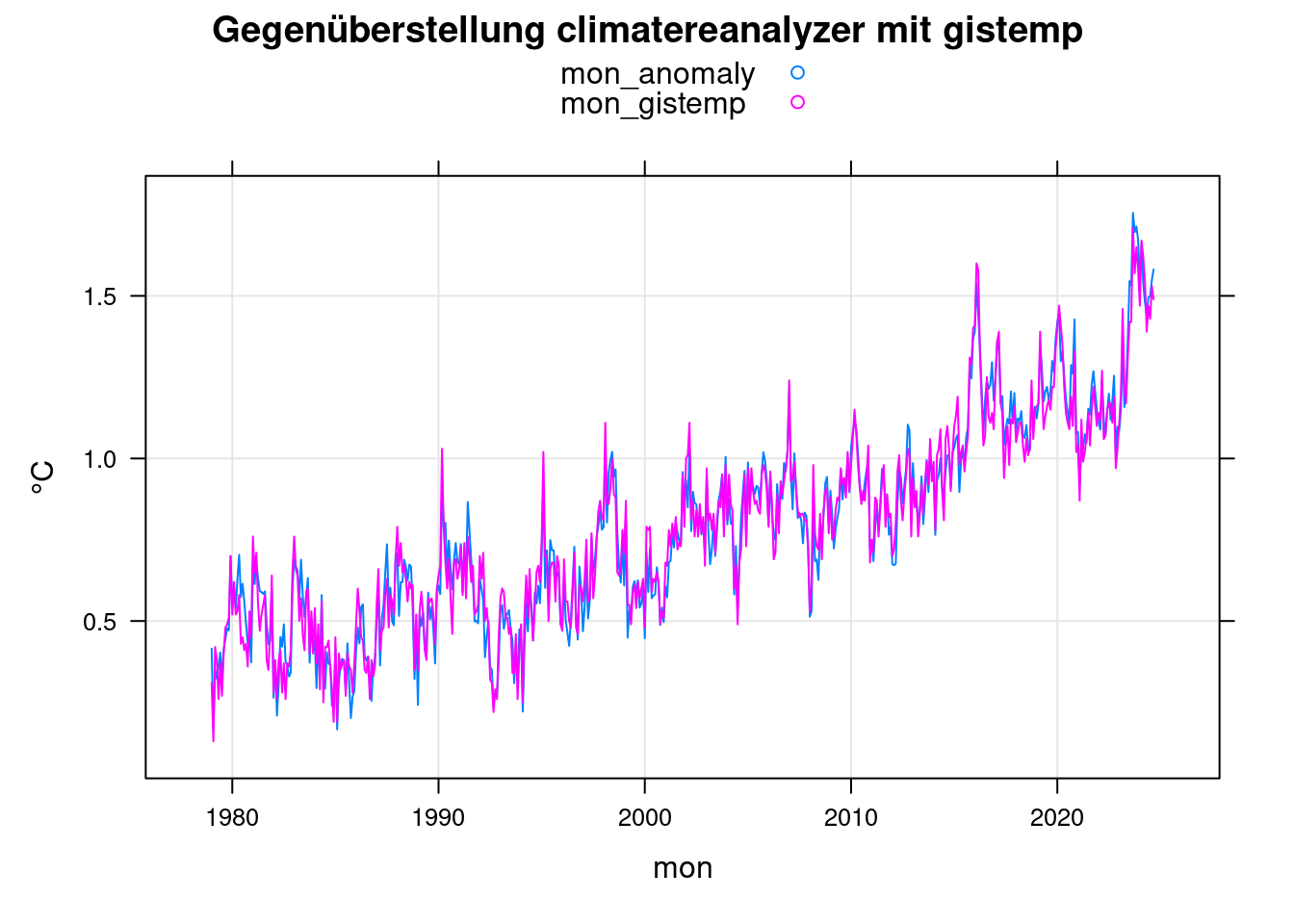

xyplot(mon_anomaly+mon_gistemp~mon, data = mon, ylab='°C',
       main = 'Gegenüberstellung climatereanalyzer mit gistemp Ausschnitt', type=c('l','g'),
       auto.key=TRUE, xlim=c(2010,max(mon$mon)));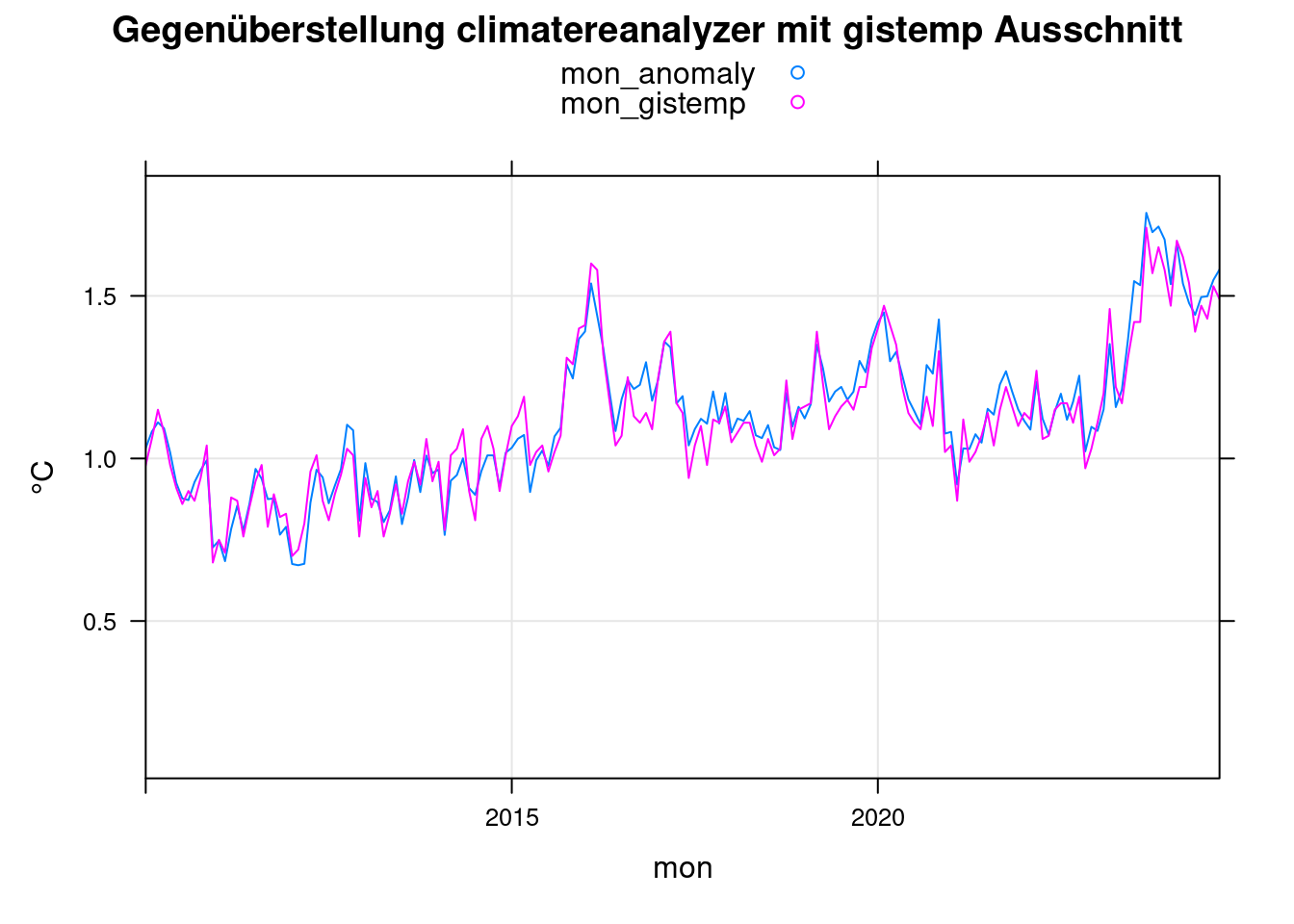

19.1 Modell basierend auf gistemp Daten

Entsprechend können wir auch auf der Basis der gistemp-Daten ein Modell basierend auf CO2, ENSO und Sonnenflecken berechnen:

mon_enso <- 1;

i = 1; # raw_enso$year[1] == 1979
n = 0;
while (i <= length(raw_enso$year))
{
    mon_enso[(n+1)] <- raw_enso$V2[i];
    mon_enso[(n+2)] <- raw_enso$V3[i];
    mon_enso[(n+3)] <- raw_enso$V4[i];
    mon_enso[(n+4)] <- raw_enso$V5[i];
    mon_enso[(n+5)] <- raw_enso$V6[i];
    mon_enso[(n+6)] <- raw_enso$V7[i];
    mon_enso[(n+7)] <- raw_enso$V8[i];
    mon_enso[(n+8)] <- raw_enso$V9[i];
    mon_enso[(n+9)] <- raw_enso$V10[i];
    mon_enso[(n+10)] <- raw_enso$V11[i];
    mon_enso[(n+11)] <- raw_enso$V12[i];
    mon_enso[(n+12)] <- raw_enso$V13[i];
    i <- i+1;
    n <- n+12;
}

# The last enso record might only contain data for one month. Fill up with last valid information
i <- length(mon_enso)-11;
while (i<=length(mon_enso)) {
   if (mon_enso[i] <= -998)
   {
       mon_enso[i] <- mon_enso[i-1];
   }
   i <- i+1;
}

mon$mon_enso <- mon_enso[1:length(mon$mon_gistemp)];
mon$mon_co2 <- day2mon(co2)[1:length(mon_gistemp)];
mon$mon_sunspots <- day2mon(sunspots)[1:length(mon_gistemp)];
mon$mon_pinatubo <- day2mon(pinatubo)[1:length(mon_gistemp)];

mfit <- nls(mon_gistemp ~ A + B*log(mon_co2/280) + C*mon_enso +D*mon_sunspots +E*mon_pinatubo, data=mon,
            start = list( A=mean(mon$mon_anomaly), B=0.01, C=0, D=0, E=-0.1) );
mfit;
## Nonlinear regression model
##   model: mon_gistemp ~ A + B * log(mon_co2/280) + C * mon_enso + D * mon_sunspots +     E * mon_pinatubo
##    data: mon
##          A          B          C          D          E 
## -0.5066155  4.3250682  0.0644451  0.0005231 -0.0665268 
##  residual sum-of-squares: 8.685
## 
## Number of iterations to convergence: 1 
## Achieved convergence tolerance: 1.048e-06
plot(mon$mon, mon$mon_gistemp, type='l', col='blue', lwd=1,
     main='Modell basierend auf gistemp Daten', xlab='', ylab='°C');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
lines(predict(mfit) ~ mon$mon, type='l', col="darkgreen", lwd=3);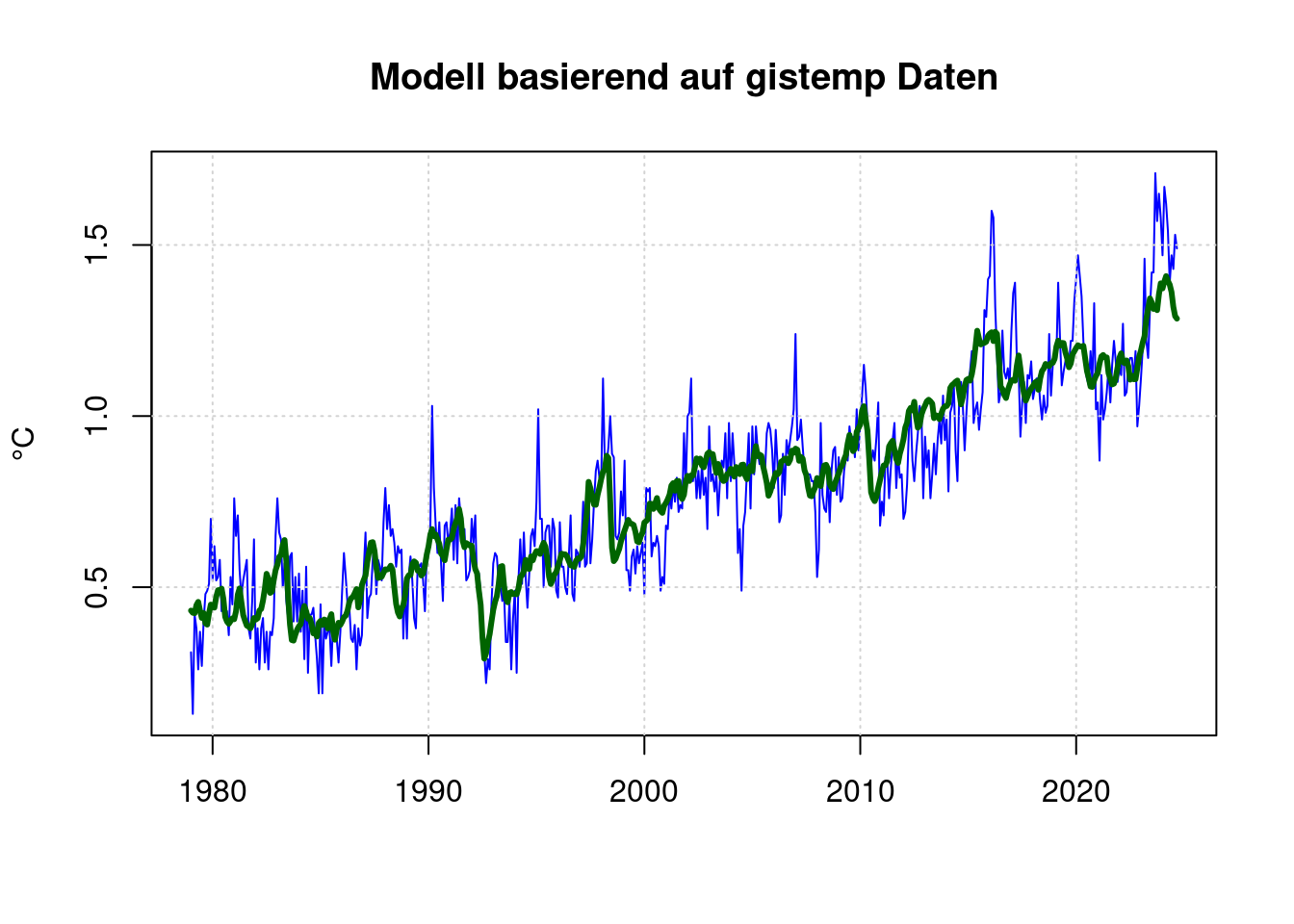

#prediction<-coef(mfit)[1]+coef(mfit)[2]*log(mon$mon_co2/280)+coef(mfit)[3]*mon$mon_enso+coef(mfit)[4]*mon$mon_sunspots+coef(mfit)[4]*mon$mon_sunspots;
#lines(prediction ~ mon$mon, type='l', col="darkgreen", lwd=3);

monval<-coef(mfit);
xyplot(mon_gistemp+(log(mon_co2/280)*monval[2]+monval[1])+mon_enso*monval[3]+mon_sunspots*monval[4]+mon_pinatubo*monval[5]~mon,
       data=mon, xlab='', ylab='°C',
       main = 'Gegenüberstellung Einflußgrößen gistemp', type=c('g','l'), auto.key=TRUE);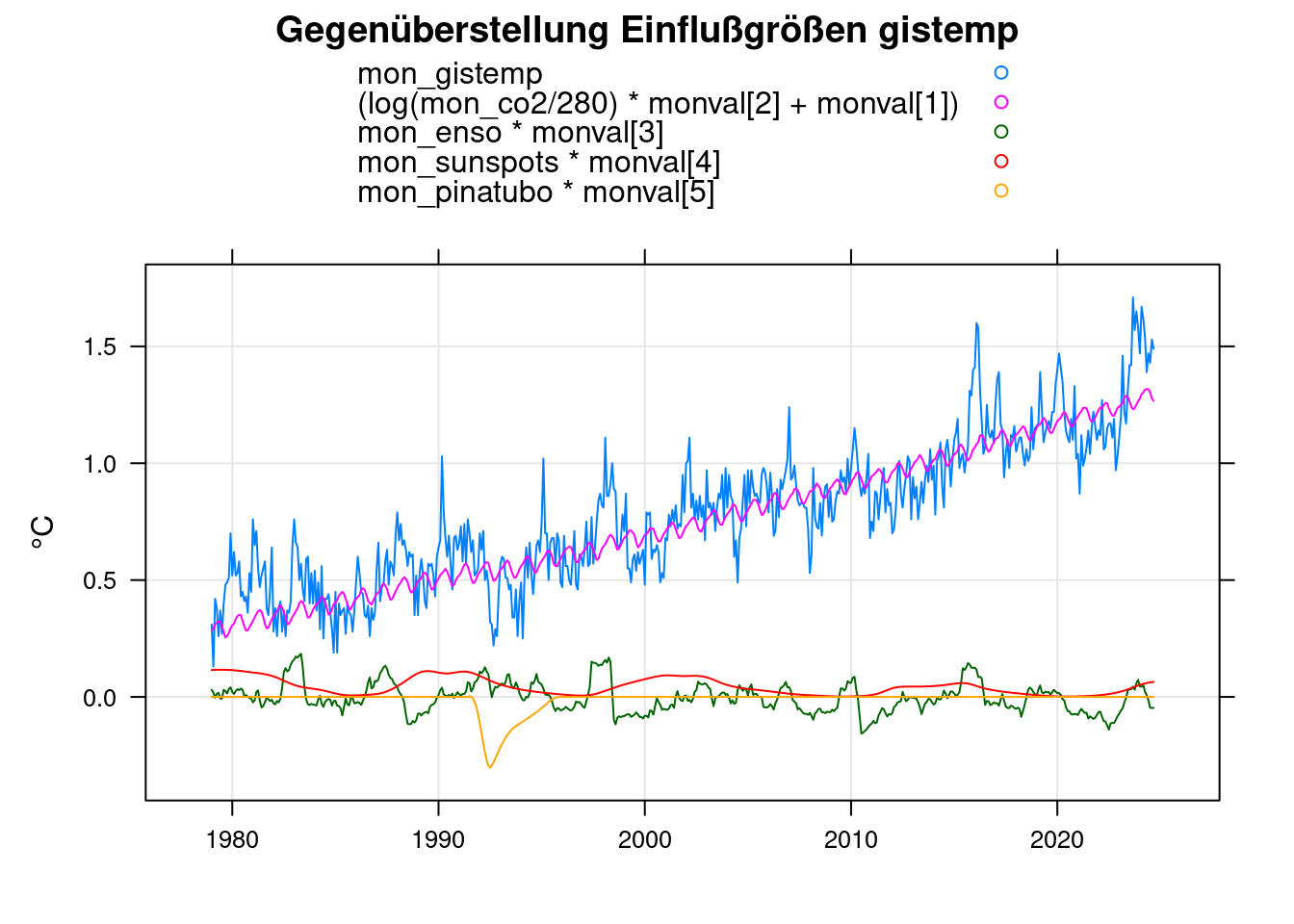

19.2 Residuum gistemp

gistemp_residuum <- mon$mon_gistemp - predict(mfit);
plot(mon$mon, gistemp_residuum, type='l', col='blue', lwd=1, xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))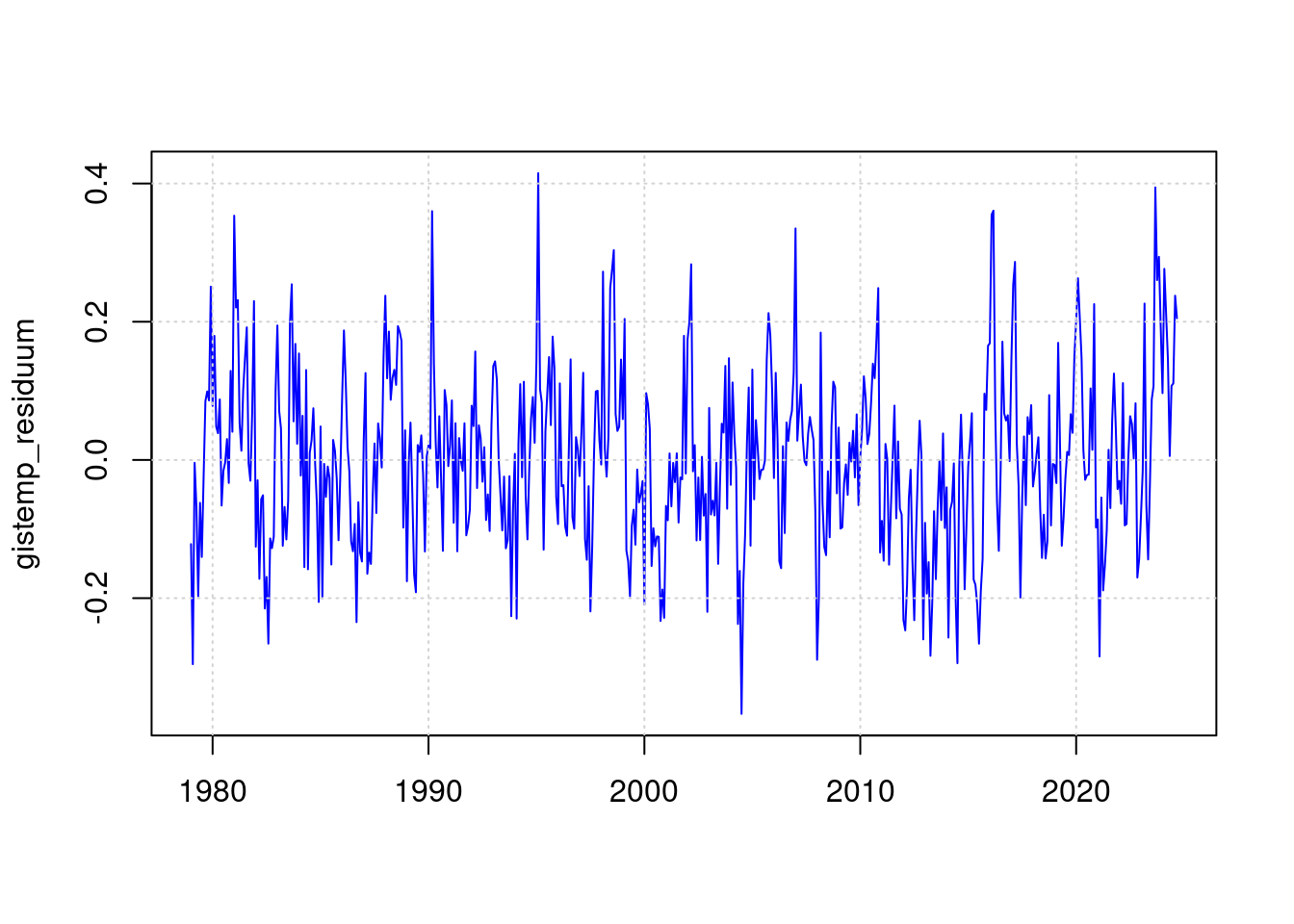

19.3 Statsitik gistemp

In den gistemp-Daten ist das Residuum des ENSO-Ereignisses von 2016 sogar größer als das von 2023. Daher bewerten wir in der Statistik den Maximalwert nur für 2023:

sd(gistemp_residuum);
## [1] 0.1258883
max(gistemp_residuum);
## [1] 0.4149645
# Maximalwert für 2023
gmax <- max(gistemp_residuum[(length(gistemp_residuum)-12):(length(gistemp_residuum))]);
gmax;
## [1] 0.3943946
gmax / sd(gistemp_residuum);
## [1] 3.132894
pnorm(-gmax/sd(gistemp_residuum)) * length(gistemp_residuum);
## [1] 0.4751366

Das heißt, ein ein Monat mit diesem Maximalwert in einer Betrachtung ab 1979 unwahrscheinlich, aber nicht ausgeschlossen.

20 Erreichen von 1,5°C

2023 wurde die im pariser Klimaabkommen als Maximalwert festgelegte Temperaturerhögung von 1,5°C bereits kurzzeitig überschritten. Diese nur kurzfristige Überschreitung verletzt aber noch nicht die Ziele des Abkommens.

Basierend auf der durchschnittlichen Erwärmungsrate der letzten Jahrzehnte kann der voraussichtliche Zeitpunkt, wann das 1,5°C Ziel des Pariser Klimaabkommens dauerhaft verfehlt wird, abgeschätzt werden.

plot(df$t, df$fanomaly, col='blue', type='l', xlab='', ylab='°C',
     xlim=c(1979, 2065), ylim=c(0, 2.5),
     main='Erwartungswert Erwärmung linearer Trend');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
abline(lmAnomaly);
abline(h='1.5', col='gray');
abline(h='2.0', col='gray');

lmAnomaly;
## 
## Call:
## lm(formula = anomaly ~ t)
## 
## Coefficients:
## (Intercept)            t  
##   -40.18063      0.02046
# Zielüberschreitung 1,5°C
t15 <- (1.5-coef(lmAnomaly)[1]) / coef(lmAnomaly)[2]
t15;
## (Intercept) 
##    2036.853
# Zielüberschreitung 2,0°C
t20 <- (2.0-coef(lmAnomaly)[1]) / coef(lmAnomaly)[2]
t20;
## (Intercept) 
##    2061.287
abline(v=t15, lty=2);
abline(v=t20, lty=2);
text(t15, 0, sprintf('%.1f', t15));
text(t20, 0, sprintf('%.1f', t20));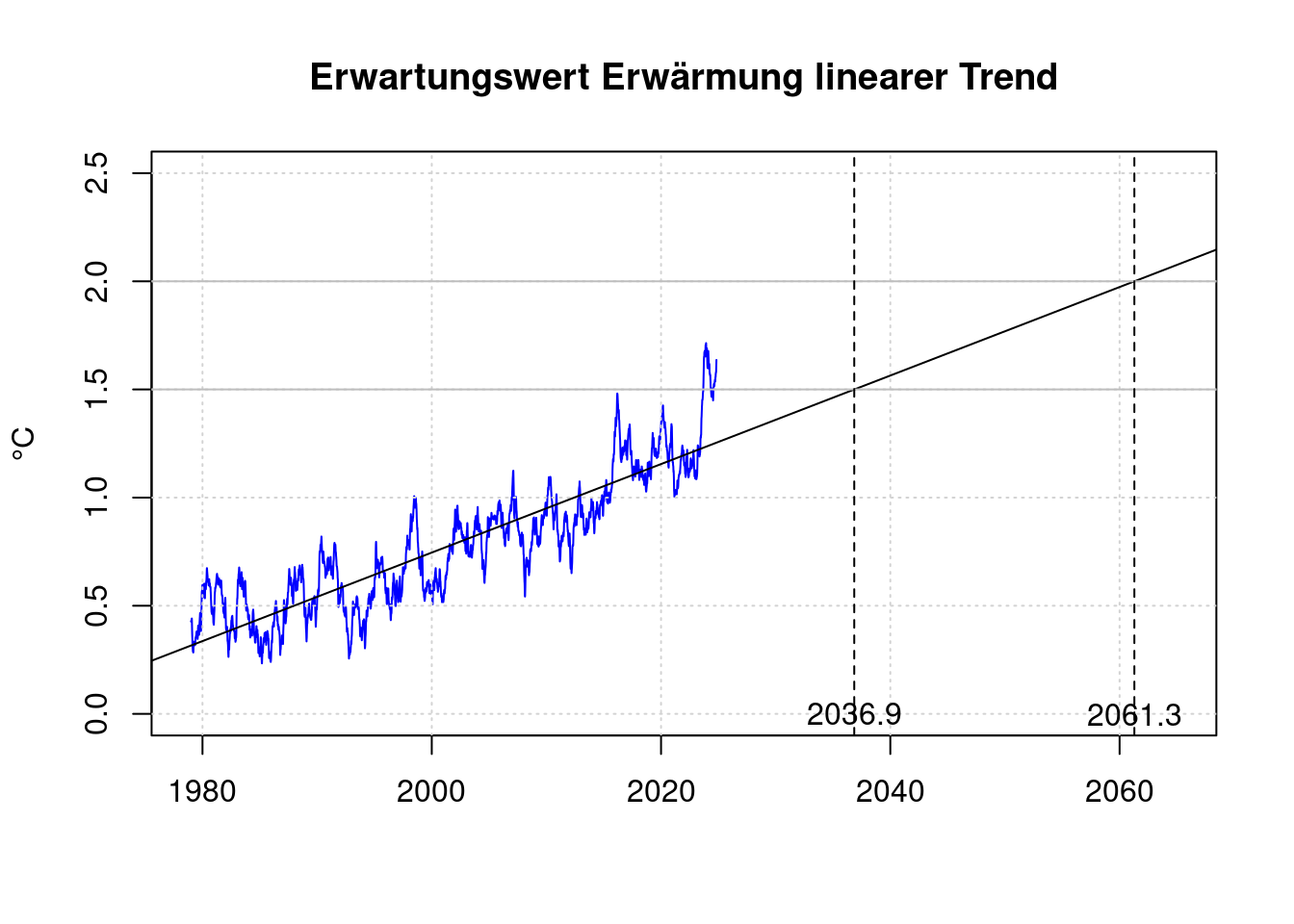

Unter der pessimistischen Annahme, dass James Hansen recht behält, und sich die Klimaerwärmung erheblich beschleunigt hätte, würde das Ziel schneller verfehlt. Hansen et. al. geben ihre Auffassung von der Erwärmung ab 2010 als mindestens 0,27°C je Jahrzehnt an:

plot(df$t, df$fanomaly, col='blue', type='l', xlab='', ylab='°C',
     xlim=c(1979, 2065), ylim=c(0, 2.5),
     main='Erwartungswert Erwärmung Hansen');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
abline(h='1.5', col='gray');
abline(h='2.0', col='gray');
shansen <- subset(df, t>2010);
#lmHansen = lm(anomaly ~ t, data=shansen);
#lmHansen;
#co <- coef(lmHansen);
hansen_co2 <- 0.27/10;
hansen_co1 <- mean(shansen$anomaly)-mean(c(shansen$t[1], shansen$t[length(shansen$t)]))*hansen_co2;
co <- c(hansen_co1, hansen_co2);
# Zielüberschreitung 1,5°C
h15 <- (1.5-co[1]) / co[2];
h15;
## [1] 2031.379
# Zielüberschreitung 2,0°C
h20 <- (2.0-co[1]) / co[2]
h20;
## [1] 2049.897
lines(c(shansen$t[1], 2070),
      c(co[1] + co[2] * shansen$t[1], co[1] + co[2] * 2070),
      col='darkred');
lines(c(shansen$t[1], shansen$t[length(shansen$t)]),
      c(mean(shansen$anomaly), mean(shansen$anomaly)),
      col='gray', lty=2);
abline(v=h15, lty=2, col='darkred');
abline(v=h20, lty=2, col='darkred');
text(h15, 0, sprintf('%.1f', h15), col='darkred');
text(h20, 0, sprintf('%.1f', h20), col='darkred');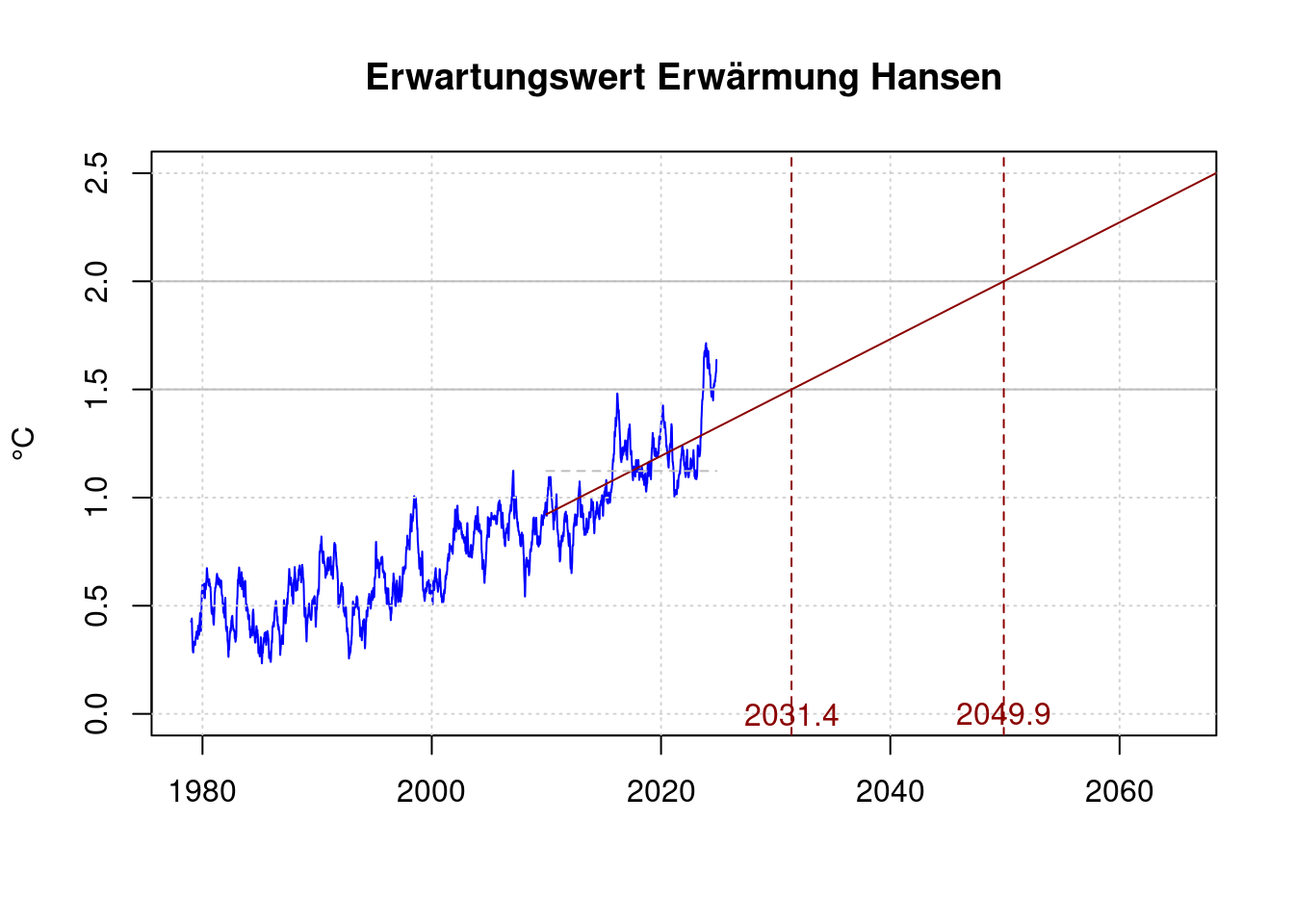

21 CO2 Modell-Überlegungen

Die gemessene Temperatur wird lt. den Modellrechnungen vor Allem von den CO2-Emissionen beeinflusst. ENSO und Sonnenflecken sind zyklische Phänomene, bei denen kein langfristiger Trend zu erwarten ist.

Daher betrachten wir die CO2-Pegel näher, um damit genauere Aussagen zur Entwicklung der Erwärmung zu machen.

Der CO2-Pegel in der Atmosphäre wird hauptsächlich durch neue Emissionen erhöht. Er ist also näherungsweise das Integral der weltweiten Emissionen. Die jährlichen Emissionen haben in den letzten Jahrzehnten zugenommen, daher reicht ein lineares Modell für die CO2-Emissionen nicht aus.

co2fit <- nls(co2 ~ A + B*t + C*t*t, data = df,
            start = list( A=400, B=0.01, C=0) );
co2fit;
## Nonlinear regression model
##   model: co2 ~ A + B * t + C * t * t
##    data: df
##          A          B          C 
##  6.104e+04 -6.251e+01  1.609e-02 
##  residual sum-of-squares: 89119
## 
## Number of iterations to convergence: 2 
## Achieved convergence tolerance: 8.016e-07
plot(df$t, df$co2, main="Historische CO2-Messungen und Modell", type='l', xlab='');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
lines(df$t, predict(co2fit), col='darkgreen');
#co2_prediction<-coef(co2fit)[1]+coef(co2fit)[2]*df$t+coef(co2fit)[3]*df$t*t;
#lines(df$t, co2_prediction, col='darkgreen');
abline(lm(co2~t, data=df), col='darkred');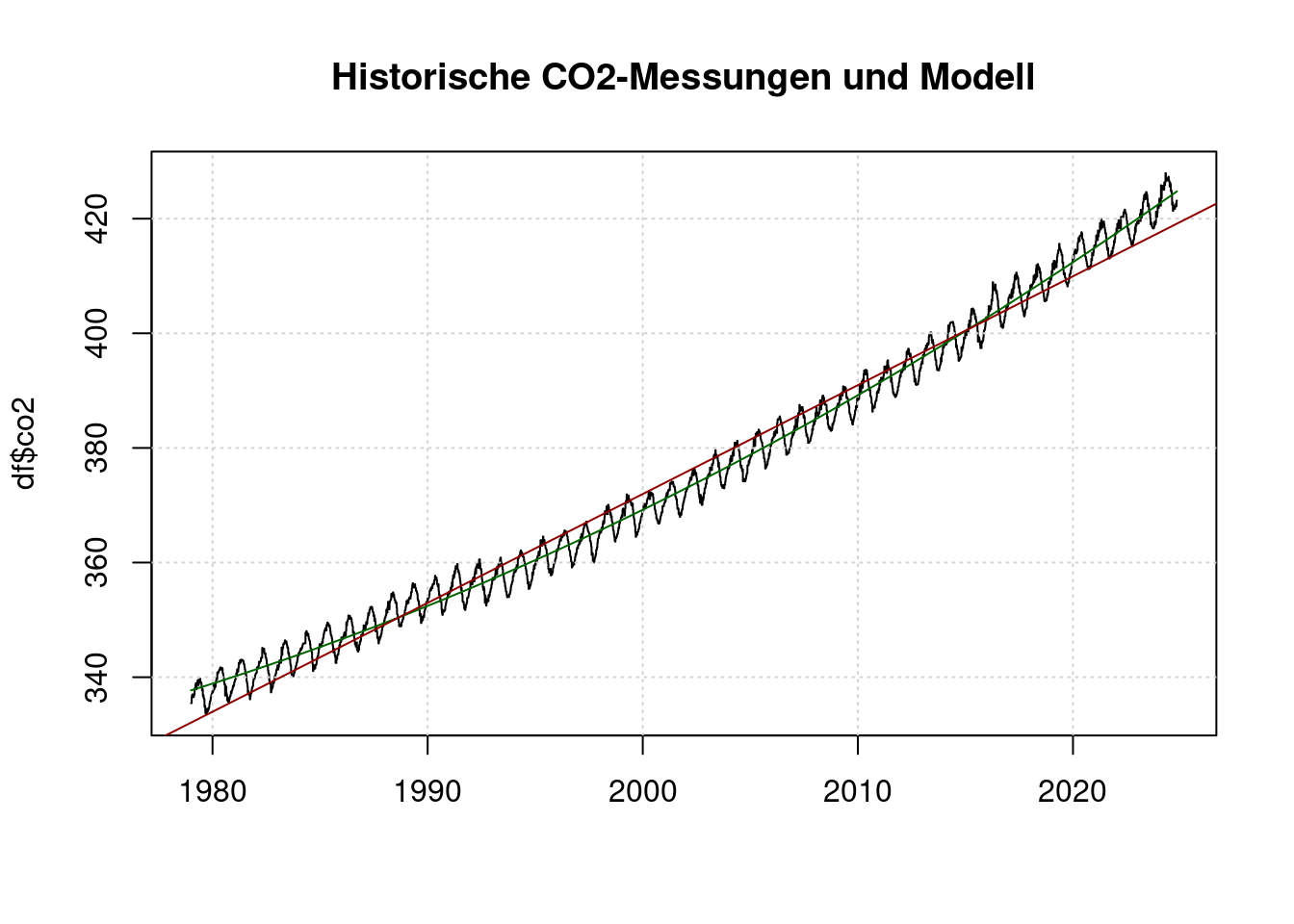

Die rote Linie ist ein lineares Modell und trifft die Messungen nicht gut. Die grüne Linie ist ein quadtratisches Modell und trifft die Messungen brauchbar.

Die CO2-Konzentration als Funktion der Zeit wird abgebildet als: \[co2 = A + B t + C t^2\]

Mit

\[\begin{align*} temp &= \ln(co2) \cdot fval[2] \\ &= \ln(A + B t + C t^2) \cdot fval[2] \\ \end{align*}\]

Ist daher die Steigung und damit die Temperaturerhöhung pro Jahr:

\[\begin{align*} \frac{dtemp}{dt} &= fval[2] \cdot \frac{1}{A + B t + C t^2} \cdot (B + 2 \cdot C \cdot t) \\ &= fval[2] \cdot \frac{B + 2 \cdot C \cdot t}{A + B t + C t^2} \\ \end{align*}\]

Damit ist für den Zeitpunkt tnow=Oktober 2024 die zu erwartende Temperaturerhöhung pro Jahrzehnt:

tnow <- 2024+(10-1)/12
per1 <- fval[2] * (coef(co2fit)[2] + 2 * coef(co2fit)[3] * tnow) /
                  (coef(co2fit)[1] + coef(co2fit)[2]*tnow + coef(co2fit)[3]*tnow^2);
per1*10;
##        B 
## 0.292408

Dies liegt noch über den Werten von James Hansen et al.

plot(df$t, df$fanomaly, col='blue', type='l', xlab='', ylab='°C',
     xlim=c(1979, 2065), ylim=c(0, 2.5),
     main='Erwartungswert Erwärmung CO2-Modell');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
abline(h='1.5', col='gray');
abline(h='2.0', col='gray');
model_co2 <- per1;
model_co1 <- mean(shansen$anomaly)-mean(c(shansen$t[1], shansen$t[length(shansen$t)]))*model_co2;
co <- c(model_co1, model_co2);
# Zielüberschreitung 1,5°C
m15 <- (1.5-co[1]) / co[2];
# Zielüberschreitung 2,0°C
m20 <- (2.0-co[1]) / co[2]
data.frame(m15, m20);
##        m15      m20
## B 2030.309 2047.408
lines(c(shansen$t[1], 2070),
      c(co[1] + co[2] * shansen$t[1], co[1] + co[2] * 2070),
      col='red');
abline(v=m15, lty=2, col='red');
abline(v=m20, lty=2, col='red');
lines(df$t, fval[1]+log(predict(co2fit)/280)*fval[2], col='darkgreen');
#co2_prediction<-coef(co2fit)[1]+coef(co2fit)[2]*df$t+coef(co2fit)[3]*df$t*t;
#lines(df$t, fval[1]+log(co2_prediction/280)*fval[2], col='darkgreen');
text(m15, 0, sprintf('%.1f', m15), col='red');
text(m20, 0, sprintf('%.1f', m20), col='red');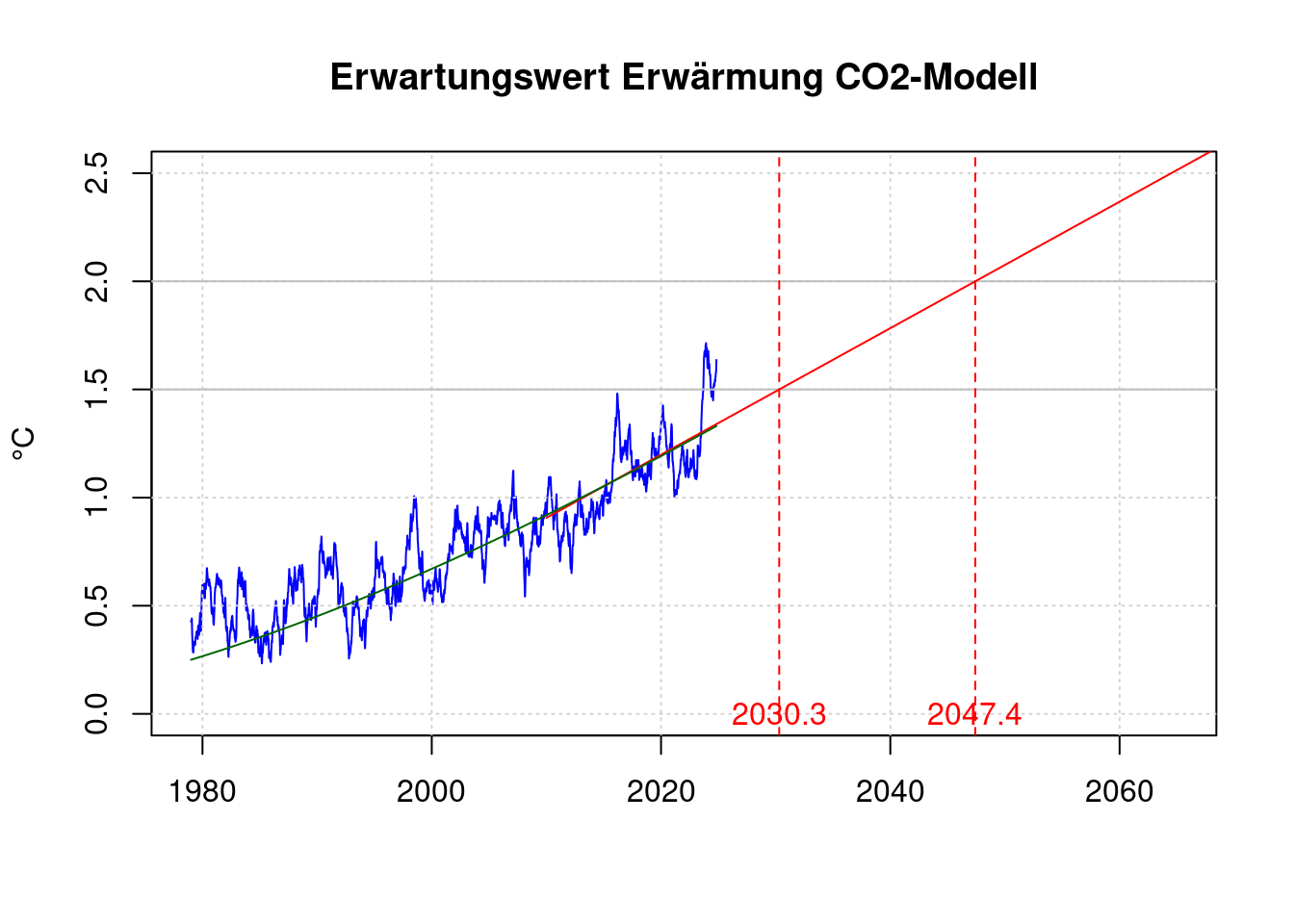

Statt des CO2 Koeffizienten des Modells als CO2, ENSO und Sonnenflecken können wir auch ein Modell nur basierend auf CO2 berechnen:

ofit <- nls(anomaly ~ A + B*log(fco2/280), data = df,
            start = list( A=mean(df$anomaly), B=0.01) );
#ofit <- ffit;
ofit;
## Nonlinear regression model
##   model: anomaly ~ A + B * log(fco2/280)
##    data: df
##       A       B 
## -0.4066  4.1041 
##  residual sum-of-squares: 574.6
## 
## Number of iterations to convergence: 1 
## Achieved convergence tolerance: 6.785e-08
oval=coef(ofit);

oper1 <- oval[2] * (coef(co2fit)[2] + 2 * coef(co2fit)[3] * tnow) /
                   (coef(co2fit)[1] + coef(co2fit)[2]*tnow + coef(co2fit)[3]*tnow^2);
oper1*10;
##         B 
## 0.2546386
plot(df$t, df$fanomaly, col='blue', type='l', xlab='', ylab='°C',
     xlim=c(1979, 2065), ylim=c(0, 2.5),
     main='Erwartungswert CO2-Modell ohne ENSO und Sonnenflecken');
grid(col = "lightgray", lty = "dotted", lwd = par("lwd"))
abline(h='1.5', col='gray');
abline(h='2.0', col='gray');

co2co<-coef(co2fit);

model_co2 <- oper1;
#model_co1 <- mean(shansen$anomaly)-mean(c(shansen$t[1], shansen$t[length(shansen$t)]))*model_co2;
#model_co1 <- oval[1] + oval[2] * (co2co[1]+co2co[2]*2024+co2co[3]*2024^2) - 2024*model_co2;
model_co1 <- oval[1] + oval[2] * log((co2co[1]+co2co[2]*2024+co2co[3]*2024^2)/280) - 2024*model_co2;

co <- c(model_co1, model_co2);
# Zielüberschreitung 1,5°C
o15 <- (1.5-co[1]) / co[2];
# Zielüberschreitung 2,0°C
o20 <- (2.0-co[1]) / co[2]
data.frame(o15, o20);
##        o15      o20
## A 2032.535 2052.171
lines(c(shansen$t[1], 2070),
      c(co[1] + co[2] * shansen$t[1], co[1] + co[2] * 2070),
      col='red');
abline(v=o15, lty=2, col='red');
abline(v=o20, lty=2, col='red');
lines(df$t, oval[1]+log(predict(co2fit)/280)*oval[2], col='darkgreen');
#lines(df$t, oval[1]+log(co2_prediction/280)*oval[2], col='darkgreen');
lines(df$t, predict(ofit));
#lines(df$t, coef(ofit)[1] + coef(ofit)[2]*log(df$fco2/280));
text(o15, 0, sprintf('%.1f', o15), col='red');
text(o20, 0, sprintf('%.1f', o20), col='red');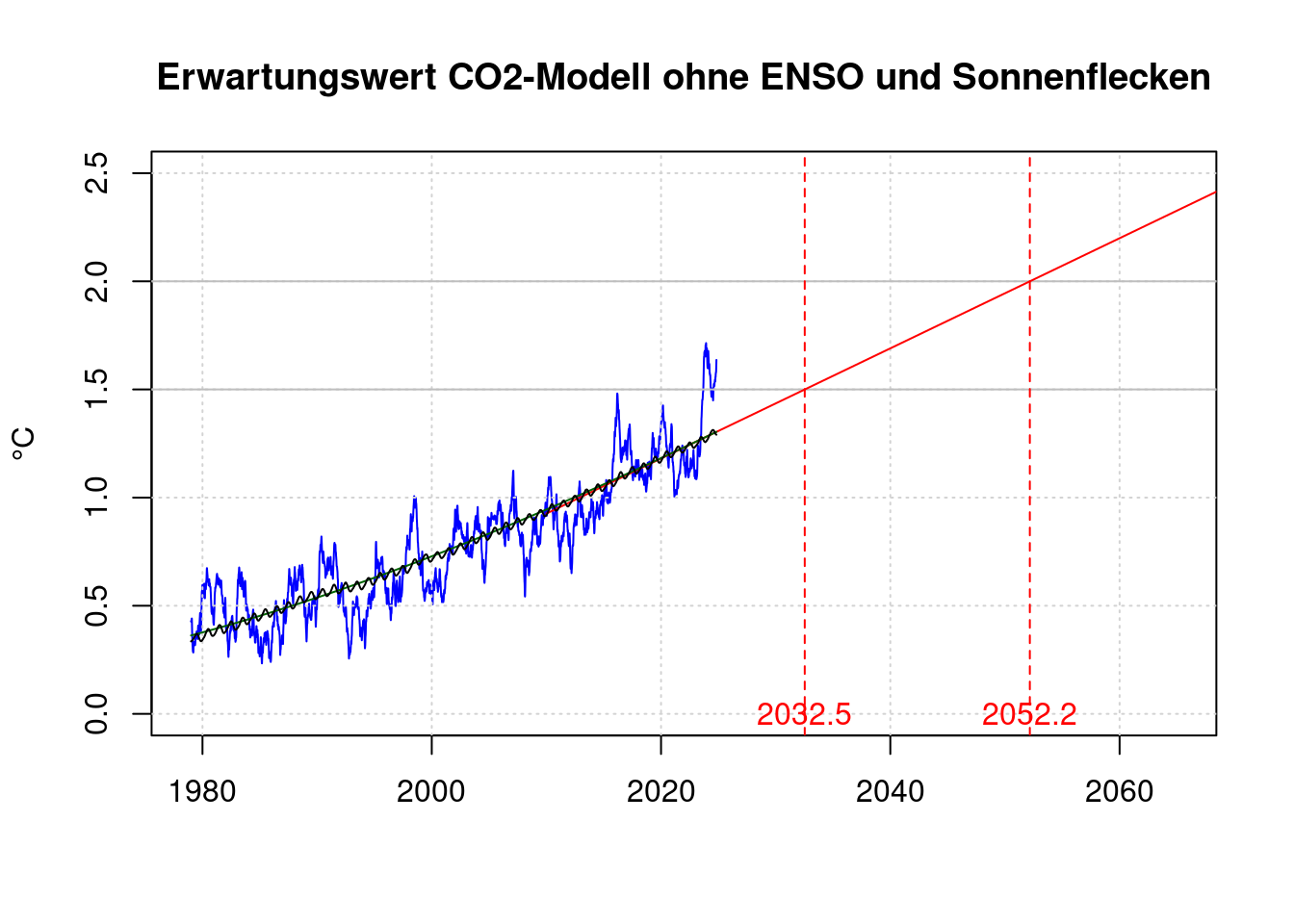

22 Ausblick

Bei einem starke El Niño Ereignis hat der ENSO-Index bislang Werte bis 2,89 erreicht. Werte von 2,5 gab seit Beginn der Zeitreihe 1979 an 181 Tagen. Ende 2023 ist der ENSO-Index 0,81. Eine Erhöhung von 0,81 auf 2,5 ergibt über das Modell pfit eine zusätzliche Temperaturerhöhung:

delta_enso <- 2.5 - enso[length(enso)];
delta_temp <- delta_enso * coef(pfit)[3];
expected_max_temp <- mean(anomaly[(length(anomaly)-31):(length(anomaly))]) + delta_temp;
data.frame(delta_temp, expected_max_temp);
##   delta_temp expected_max_temp
## C  0.3425192          2.023917

Allerdings ist die Schätzung des Klimawissenschaftlers Gavin Schmidt https://www.realclimate.org/index.php/archives/2024/01/annual-gmsat-predictions-and-enso/ für 2024 “nur” 1,38 ± 0,14°C für das gesamte Jahr.

Die durchschnittliche Temperaturerhöhung im 2. Halbjahr 2023 betrug in °C:

measured_temp_2023 <- mean(anomaly[(length(anomaly)-182):(length(anomaly))]);
measured_temp_2023;
## [1] 1.542276

Bei der konservativen Annahme, dass die Erwärmung so weitergeht, wie dies seit 1979 geschah, dauert es bis

lm_temp_2023 <- coef(lmAnomaly)[1] + coef(lmAnomaly)[2] * tnow;
(measured_temp_2023 - lm_temp_2023) / coef(lmAnomaly)[2] + tnow;
## (Intercept) 
##    2038.919

, bis die Erwärmung, die wir 2023 als extrem erlebt haben (man denke nur an die Überschwemmungen in Niedersachsen um Weihnachten 2023) der regelmäßige Normallfall sein werden.

Zusätzliche Erwärmung durch gelegentliche El Niño Ereignisse kommen dann noch dazu.

23 Klimasensitivität

Die Klimasensitivität ist definiert als die Erwärmung der Erde in °C, die bei einer Verdoppelung der CO2-Konzentration in der Luft auftritt, wenn diese neue Konzentration dann längere Zeit konstant bleibt.

Die Beste Schätzung des IPCC beträgt 3°C. Hansen et al. schätzt die Klimasensitivität der Erde stattdessen in ihrer neuesten Arbeit auf ca. 4,8°C.

Die CO2-Konzentration der Luft vor Beginn der Industrialisierung wird auf 280ppm geschätzt. Die derzeitige CO2-Konzentration in ppm beträgt:

co2_2023 <- mean(df$co2[length(df$co2)-365], df$co2[length(df$co2)]);
co2_2023;
## [1] 419.05

Die Erwärmung temp ist dabei logarithmisch von der CO2-Konzentration co2 und der Klimasensitivität ecs abhängig.

\[temp = ecs \cdot \log_2\frac{co2}{280}\]

Bei einer Klimasensitivität von 3,0°C, wie vom IPCC geschätzt, wäre die nach langer Einschwingzeit zu erwartende Erwärmung in °C demnach:

ecs <- 3.0;
ecs * log2(co2_2023/280);
## [1] 1.745087

Bei einer Klimasensitivität von 4,8°C, wie von Hansen vermutet, wäre sie:

ecs <- 4.8;
ecs * log2(co2_2023/280);
## [1] 2.792139

Die im pfit-Modell aus den Daten geschätzte Abhängigkeit der Temperatur ist ebenfalls ein Schätzwert für die Klimasensitivität. Allerdings berücksichtigt er die lange Einschwingzeit nicht und unterschätzt daher möglicherweise die Erwärmung.

\[\begin{align*} temp & = pval[2] \cdot \ln \frac{co2}{280} \\ & = ecs \cdot \log_2\frac{co2}{280} \\ & = ecs \cdot \frac{\ln\frac{co2}{280}}{\ln 2} \\ ecs & = \ln 2 \cdot pval[2] \\ \end{align*}\]

ecs <- log(2) * coef(pfit)[2];
ecs;
##        B 
## 3.198625
ecs * log2(co2_2023/280);
##        B 
## 1.860626

Demnach ist nach diesem Modell bereits jetzt eine Erwärmung von 1,83 °C zu erwarten, die tatsächliche Temperatur in den letzten Jahren war aber niedriger.

xyplot(anomaly~t, data = df, ylab='°C', xlim=c(2017, 2025), xlab='',
       main = 'Temperaturen der letzten Jahre.', type='l', auto.key=TRUE);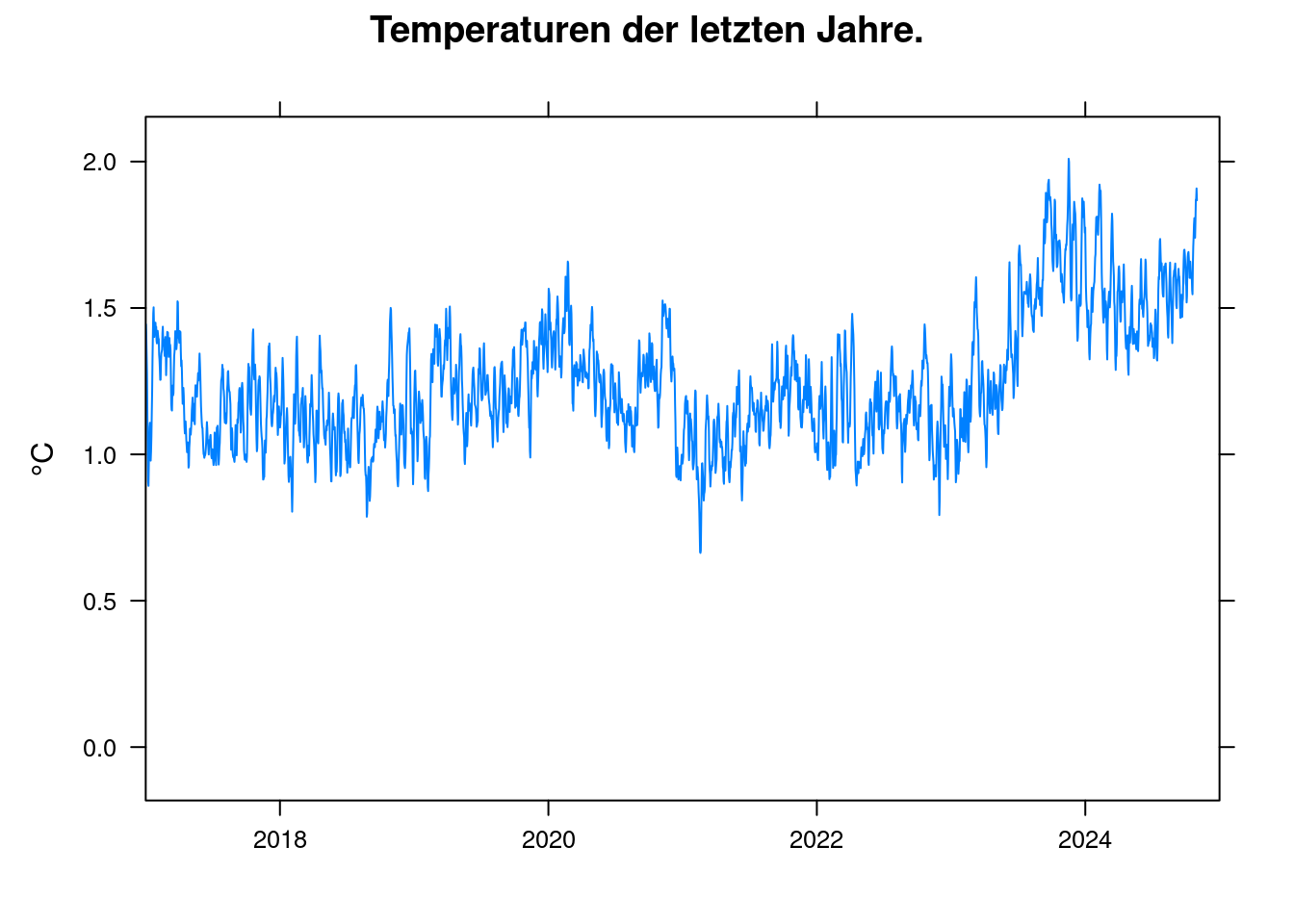

Das dürfte im Wesentlichen an zwei Faktoren liegen:

xyplot(enso~t, data = df, ylab='°C', xlim=c(2017, 2025), xlab='',
       main = 'El Niño Southern Oscillation Index der letzten Jahre.', type='l', auto.key=TRUE);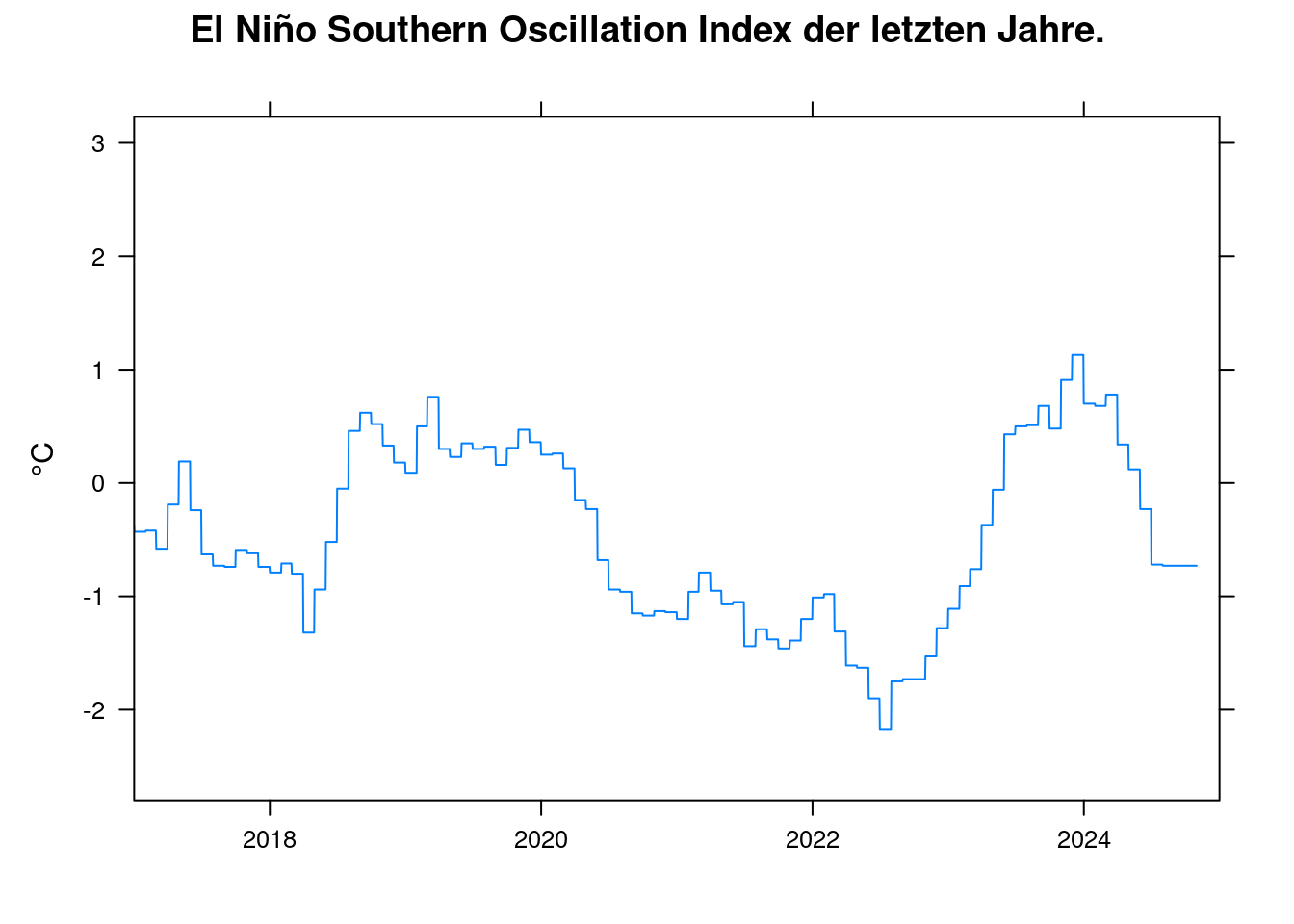

Nach dem pfit-Modell verursacht eine Anstieg des ENSO-Index von -2 auf +2 eine Temperaturerhöhung in °C:

coef(pfit)[3] * (2 - -2);
##         C 
## 0.4241724

24 Fazit

Zunächst mal ist es wenig überraschend, dass die Erde sich wie seit Jahrzehnten vorhergesagt erwärmt. Die zugrundelegenden Mechanismen sind wissenschaftlich gut verstanden und lassen auch Aussagen über die Zukunft zu.

Nur eine radikale Veränderung der Lebens- und Wirtschaftsweise mit dem Ziel der Reduktion von CO2 und anderen Treibhausgasen könnte eine Verletzung des Pariser Klimaschutzabkommens und damit eine Notlage für die nächsten Generationen noch verhindern.

Man kann ziemlich sicher erkennen, dass sich die Erwärmung in den letzten Jahren beschleunigt hat und dass wir umso schneller den Bereich des Pariser Klimaabkommens verlassen werden. Dafür reicht aber eine Betrachtung der Beschleunigung der CO2-Emissionen aus, die von Hansen et al. postulierte höhere Klimasensitivität, die durch SO2-Emissionen kaschiert wird, ist dafür nicht notwendig.

2023 war tatsächlich unerwartet warm, jedoch muss diese begrenzte Steigerung nicht zwangsläufig auf einen zusätzlichen Faktor zurückgehen, sie könnte auch einfach Wetter sein. Die Erwärmung von 2023 könnte aber auch auf eine mögliche noch zusätzliche Komponente hindeuten viele Klimawissenschaftler sagen, dass dies genauer erforscht werden sollte. Sie ist aber nicht so extrem, wie stellenweise im Internet behauptet wird.

Die 2023 Meßergebnisse sind jedenfalls alleine kein zwingender Grund zu der von Hansen postulierten Annahme, dass der IPCC seit Jahrzehnten die Klimasensitivität derartig gravierend unterschätzen würde.

Ich schließe mich daher eher der Auffassung von Michael E. Mann an: Es findet bekanntermaßen eine gefährliche Klimaerwärmung statt und die Menschheit muss unbedingt intensive Maßnahmen veranlassen, um diese Veränderung aufzuhalten. Aber der pessimistische Ausblick von James E. Hansens jüngster Arbeit ist meiner Meinung nach voreilig.

Firmenlogo

Letzte News